Câu 1.19 trang 10 sách bài tập Đại số và Giải tích 11 Nâng cao. Phép đối xứng qua đường thẳng có phương trình \(y = 1\) biến đồ thị của mỗi hàm số sau thành đồ thị của hàm số nào. Bài 1: Các hàm số lượng giác
Phép đối xứng qua đường thẳng có phương trình \(y = 1\) biến đồ thị của mỗi hàm số sau thành đồ thị của hàm số nào :
a) \(y = \sin x\)
b) \(y = \cos x + 1\)
c) \(y = \sin {x \over 2} + 2\)
Vẽ đồ thị của hàm số tìm được.
Giải
Điểm đối xứng \(M\left( {x;y} \right)\) qua đường thẳng \(y = 1\) là điểm \(M’\left( {x’;y’} \right),x’ = x,y’ = y,\) tức là \(x = x’,y = 2 - y’.\) Vậy ta có:
Advertisements (Quảng cáo)
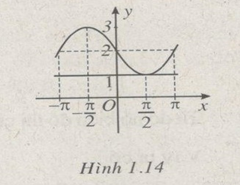
a) \(y = 2 - \sin x\) (h.1.14)
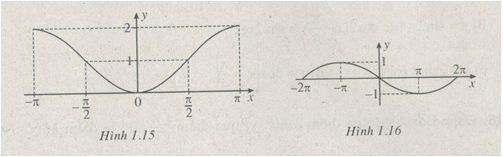
b) \(y = 1 - \cos x\) (h.1.15)
c) \(y = - \sin {x \over 2}\) (h.1.16)
