Chứng minh:
a) Điểm có tọa độ \(\left( {k\pi ;0} \right)\) (k là một số nguyên) là tâm đối xứng của đồ thị hàm số \(y = \sin x\)
b) Điểm có tọa độ \(\left( {{{k\pi } \over 2};0} \right)\) (k là một số nguyên) là tâm đối xứng của đồ thị hàm số \(y = \tan x\)
c) Đường thẳng có phương trình \(x = k\pi \) (k là một số nguyên) là trục đối xứng của đồ thị hàm số \(y = \cos x\)
Giải
a) Điểm \(M’\left( {x’;y’} \right)\) là điểm đối xứng của điểm \(M\left( {x;y} \right)\) qua điểm \(\left( {k\pi ;0} \right)\) khi và chỉ khi:
\({{x + x’} \over 2} = k\pi ,{{y + y’} \over 2} = 0,\) tức là
\(\left\{ \matrix{
x’ = - x + k2\pi \hfill \cr
y’ = y \hfill \cr} \right.\)
Gọi C là đồ thị hàm số \(y = \sin x\). C nhận \(\left( {k\pi ;0} \right)\) làm tâm đối xứng khi và chỉ khi: Với mọi điểm \(M\left( {x;y} \right)\) thuộc C (tức là với mọi \(x,y = \sin x\)) điểm \(M’\left( {x’;y’} \right)\) nói trên (tức là \(x’ = - x + k2\pi ,y’ = - y)\) cũng thuộc C; điều này có nghĩa là \( - \sin x = \sin \left( {x + k2\pi } \right),\) với mọi \(x \in Z\) là một tâm đối xứng của đồ thị C của hàm số \(y = \sin x\)
Cách chứng minh khác:
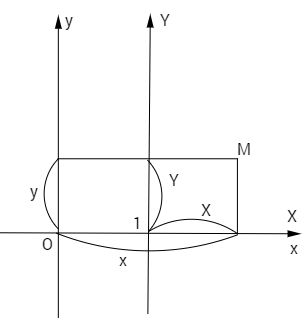
Xét phép đổi trục tọa độ Oxy sang trục hệ tọa độ IXY, với \(I\left( {k\pi ;0} \right);x = X + k\pi ;y = Y\) (phép biến đổi gốc tọa độ), (h.vẽ) thì đồ thị của hàm số \(y = \sin x\) trong hệ trục tọa độ Oxy là đồ thị của hàm số
\(Y = \sin \left( {X + k\pi } \right) = {\left( { - 1} \right)^k}\sin X\)
Trong hệ tọa độ IXY. Vì hàm số \(Y = {\mathop{\rm sinX}\nolimits} \) cũng như hàm số \(Y = - {\mathop{\rm sinX}\nolimits} \) là hàm số lẻ nên đồ thị nhận I là tâm đối xứng.
b) Điểm \(M’\left( {x’;y’} \right)\) là điểm đối xứng của \(M\left( {x;y} \right)\) qua điểm \(\left( {{{k\pi } \over 2};0} \right)\) khi và chỉ khi
\({{x + x’} \over 2} = {{k\pi } \over 2},{{y + y’} \over 2} = 0,\) tức là
Advertisements (Quảng cáo)
\(\left\{ \matrix{
x’ = - x + k\pi \hfill \cr
y’ = - y \hfill \cr} \right.\)
Gọi C là đồ thị của hàm số \(y = \tan x\); C nhận \(\left( {{{k\pi } \over 2};0} \right)\) làm tâm đối xứng khi và chỉ khi: Với mọi điểm \(M\left( {x;y} \right)\) thuộc C (tức là \(x \in {D_1},y = \tan x\)) điểm \(M’\left( {x’;y’} \right)\) nói trên (tức là \(x’ = - x + k\pi ,y’ = - y\)) cũng thuộc C; điều này có nghĩa là \( - \tan x = \tan \left( { - x + k\pi } \right),\) với mọi \(X \in {D_1}.\) Điều đó đúng do \(\pi \) là chu kì của hàm số \(y = \tan x\). Vậy điểm \(\left( {{{k\pi } \over 2};0} \right),k \in Z\) là một tâm đối xứng của đồ thị C của hàm số \(y = \tan x\)
Chứng minh cách khác:
Xét phép đổi trục tọa độ Oxy sang hệ trục tọa độ IXY, với \(I\left( {{{k\pi } \over 2};0} \right);x = X + {{k\pi } \over 2};y = Y.\) Đồ thị của hàm số \(y = \tan x\) trong hệ trục toạn độ Oxy là đồ thị của hàm số
\(Y = \tan \left( {X + k{\pi \over 2}} \right) = \left\{ \matrix{
\tan X\,\,\,\,\,\,\,\,\,\,neu\,\,K\text{ chẵn } \hfill \cr
- {1 \over {\tan X}}\,\,\,\,\,neu\,\,K\text{ lẻ } \hfill \cr} \right.\)
Trong hệ tọa độ IXY. Vì hàm số \(Y = \tan X\) cũng như hàm số \(Y = - {1 \over {\tan X}}\) là hàm số lẻ nên đồ thị nhận I làm tâm đối xứng.
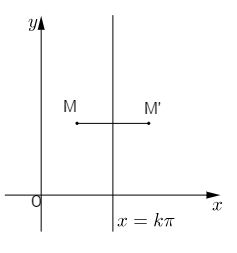
c) Điểm \(M’\left( {x’;y’} \right)\) là điểm đối xứng của điểm \(M\left( {x;y} \right)\) qua đường thẳng \(x = k\pi \) (h.vẽ) khi và chỉ khi \({{x + x’} \over 2} = k\pi ,y = y’,\) tức là
\(\left\{ \matrix{{x’} = - x + k2\pi \hfill \cr {y’} = y \hfill \cr} \right.\)
Gọi C là đồ thị của hàm số \(y = \cos x.\) C nhận đường thẳng \(x = k\pi \) làm một trục đối xứng khi và chỉ khi: Với mọi điểm \(M\left( {x;y} \right)\) thuộc C (tức là với mọi \(x,y = \cos x\)) điểm \(M’\left( {x’;y’} \right)\) nói trên cũng thuộc C. Điều này có nghĩa là
\(\cos x = \cos \left( { - x + k2\pi } \right),\forall x \in R\)
Rõ ràng ta có đẳng thức đó, do \(2\pi \) là chu kì của hàm số \(y = \cos x.\) Vậy đường thẳng \(x = k\pi ,k \in Z\) là một trục đối xứng của đồ thị C của hàm số \(y = \cos x.\).
Cách chứng minh khác
Xét phép đổi trục tọa độ Oxy sang trục toạ độ IXY, với \(I\left( {k\pi ;0} \right);x = X + k\pi ;y = Y,\) thì đồ thị của hàm số \(y = \cos x\) trong hệ trục tọa độ Oxy là đồ thị của hàm số \(Y = \cos \left( {X + k\pi } \right) = {\left( { - 1} \right)^k}\cos X\) trong hệ tọa độ IXY. Vì hàm số \(Y = \cos X\) cũng như hàm số \(Y = - \cos X\) là các hàm số chẵn nên đồ thị đó nhận trục IY (tức là đường thẳng \(x = k\pi \)) làm trục đối xứng.
