Cho hình bình hành ABCD nằm trong mặt phẳng (P) và một điểm S nằm ngoài mp(P). Gọi M là điểm nằm giữa S và A ; N là điểm giữa S và B; giao điểm của hai đường thẳng AC và BD là O. Câu 11 trang 50 SGK Hình học 11 Nâng cao - Bài 1: Đại cương về đường thẳng và mặt phẳng
Cho hình bình hành ABCD nằm trong mặt phẳng (P) và một điểm S nằm ngoài mp(P). Gọi M là điểm nằm giữa S và A ; N là điểm giữa S và B; giao điểm của hai đường thẳng AC và BD là O
a. Tìm giao điểm của mặt phẳng (CMN) với đường thẳng SO
b. Xác định giao tuyến của hai mặt phẳng (SAD) và (CMN)

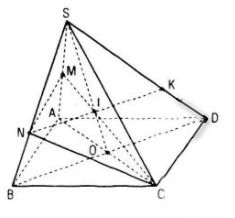
a. Tìm SO ∩ (CNM)
Advertisements (Quảng cáo)
Trong mặt phẳng (SAC) gọi I là giao điểm của SO với CM : I = SO ∩ CM
mà CM ⊂ (CMN) nên I = SO ∩ (CMN)
b. Tìm (SAD) ∩ (CMN)
Trong mp(SBD) gọi K là giao điểm của NI và SD: K = NI ∩ SD
Ta có: M, K \(\in\) (CMN) và M, K \(\in\) (SAD)
Do đó (SAD) ∩ (CMN) = MK
