Giả sử phép đối xứng tâm . Câu 14 trang 18 SGK Hình học 11 Nâng cao - Bài 4. Phép quay và phép đối xứng tâm
Bài 14. Giả sử phép đối xứng tâm \({D_O}\) biến đường thẳng d thành d’. Chứng minh
a. Nếu d không đi qua tâm đối xứng O thì d’ song song với d, O cách đều d và d’
b. Hai đường thẳng d và d’ trùng nhau khi và chỉ khi d đi qua O
Advertisements (Quảng cáo)
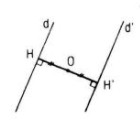
a. Kẻ \(OH ⊥ d (H ∈ d)\) thì vì d không đi qua O nên H không trùng với O
Phép đối xứng tâm \(Đ_ O\) biến H thành H’ thì O là trung điểm của HH’, và biến đường thẳng d thành đường thẳng d’ vuông góc với OH’ tại H’.
Suy ra d và d’ song song, cách đều điểm O
b. Nếu d không đi qua điểm O thì theo câu a), d’ // d nên d’ không trùng với d.
Nếu d đi qua O thì mọi điểm \(M ∈ d\) biến thành điểm \(M’ ∈ d’.\)