Advertisements (Quảng cáo)
43. Trang 11 Sách bài tập Hình Học 11 nâng cao.
Về phía ngoài của tam giác ABC vẽ các hình vuông BCMN và ACPQ có tâm O và O’.
a) Chứng minh rằng khi cố định hai điểm A, B và cho điểm C thay đổi thì đường thẳng NQ luôn luôn đi qua một điểm cố định.
b) Gọi I là trung điểm của AB. Chứng minh rằng IOO’ là tam giác vuông cân.
a) \({Q_A}\) và \({Q_B}\) lần lượt là các phép quay tâm A, B với góc quay:
\(\left( {AQ,AC} \right) = \left( {BC,BN} \right) = {90^o}.\)
Advertisements (Quảng cáo)
Theo bài 42 ta có: Hợp thành của hai phép đó là phép đối xứng qua điểm H xác định. Vì phép đối xứng tâm H biến Q thành N nên H là trung điểm của đoạn thẳng NQ, tức là đường thẳng NQ luôn luôn đi qua điểm H cố định.
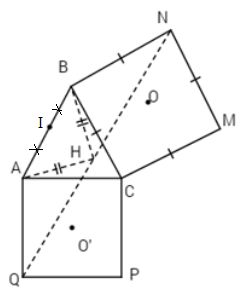
b) Gọi \({Q_O}\) và \({Q_{O’}}\) là các phép quay có góc quay \({90^o}\) với tâm quay tương ứng là O và O’ thì phép hợp thành F của chúng biến B thành A. Nhưng vì F là đối xứng tâm, nên tâm đối xứng là trung điểm I của AB. Suy ra tam giác IOO’ vuông cân tại đỉnh I.
Cách giải khác
Phép quay tâm C góc quay \({90^o}\) biến A thành P và biến M thành B. Bởi vậy, ta có AM = PB và \(AM \bot PB.\) Chú ý rằng IO là đường trung bình của tam giác ABM và IO’ là đường trung bình của tam giác APB nên suy ra IOO’ là tam giác vuông cân.