Bài 8 trang 54 sách giáo khoa hình học lớp 11: Bài 1. Đại cương về đường thẳng và mặt phẳng. Cho tứ diện ABCD. Gọi M và N lần lượt là trung điểm của các cạnh AB và CD trên cạnh AD lấy điểm P không trùng với trung điểm của AD
Bài 8. Cho tứ diện \(ABCD\). Gọi \(M\) và \(N\) lần lượt là trung điểm của các cạnh \(AB\) và \(CD\) trên cạnh \(AD\) lấy điểm \(P\) không trùng với trung điểm của \(AD\)
a) Gọi \(E\) là giao điểm của đường thẳng \(MP\) và đường thẳng \(BD\). Tìm giao tuyến của hai mặt phẳng \((PMN)\) và \((BCD)\)
b) Tìm giao điểm của mặt phẳng \((PMN)\) và \(BC\).
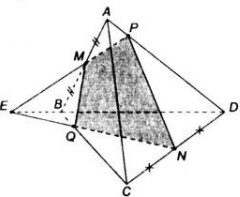
a) Ta có \(E\in BD\Rightarrow E\in(BCD)\)
\(E\in MP\Rightarrow E\in(PMN)\)
Advertisements (Quảng cáo)
Do đó: \(E\in (BCD)\cap(PMN)\)
\(N\in CD\Rightarrow N\in(BCD)\)
\(N \in(PMN)\)
Do đó: \(N\in (BCD)\cap(PMN)\)
\(=> (PMN) ⋂ (BCD) = EN\)
b) Trong mặt phẳng \((BCD)\) gọi \(Q\) là giao điểm của \(NE\) và \(BC\) thì \(Q\) là giao điểm của \((PMN)\) và \(BC\).