
Một cửa hàng ước tính số lượng sản phẩm \(q\left( {0 \le q \le 100} \right)\) bán được phụ thuộc vào giá bán \(p\) (tính bằng nghìn đồng) theo công thức \(p + 2q = 300\). Chi phí cửa hàng cần chi để nhập về \(q\) sản phẩm là
\(C\left( q \right) = 0,05{q^3} - 5,7{q^2} + 295q + 300\) (nghìn đồng).
a) Viết công thức tính lợi nhuận \(I\) của cửa hàng khi nhập về và bán được \(q\) sản phẩm.
b) Trong khoảng nào của \(q\) thì lợi nhuận sẽ tăng khi \(q\) tăng, trong khoảng nào thì lợi nhuận giảm khi \(q\) tăng?

• \(I = pq - C\).
• Xét hàm số \(I\left( q \right)\) trên đoạn $\left[ 0;100 \right]$, lập bảng biến thiên và tìm khoảng đồng biến, nghịch biến của hàm số.

Advertisements (Quảng cáo)
a) \(p + 2q = 300 \Leftrightarrow p = 300 - 2q\)
\(I = pq - C = \left( {300 - 2q} \right).q - \left( {0,05{q^3} - 5,7{q^2} + 295q + 300} \right) = - 0,05{q^3} + 3,7{q^2} + 5q - 300\).
b) Xét hàm số \(I\left( q \right) = - 0,05{q^3} + 3,7{q^2} + 5q - 300\) trên đoạn \(\left[ {0;100} \right]\).
Ta có:
\(I’\left( q \right) = - 0,15{q^2} + 7,4q + 5;I’\left( q \right) = 0 \Leftrightarrow q = 50\) hoặc \(q = - \frac{2}{3}\) (loại).
Bảng biến thiên:
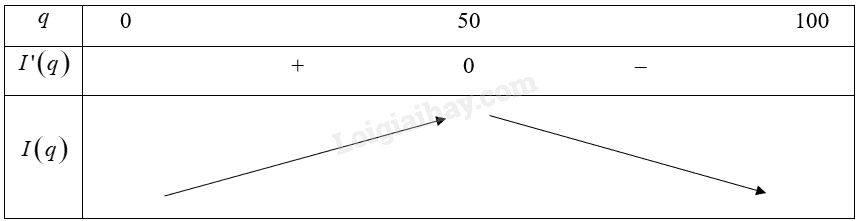
Vậy hàm số đồng biến trên khoảng \(\left( {0;50} \right)\), hàm số nghịch biến trên khoảng \(\left( {50;100} \right)\).
Vậy trong khoảng \(\left( {0;50} \right)\) lợi nhuận sẽ tăng khi \(q\) tăng, trong khoảng \(\left( {50;100} \right)\) lợi nhuận sẽ giảm khi \(q\) tăng.
