
Chọn đúng hoặc sai cho mỗi ý a, b, c, d.Lợi nhuận một xưởng thu được từ việc sản xuất một mặt hàng được cho bởi công thức \(P\left( q \right) = - {q^3} + 24{q^2} + 780q - 5000\) (nghìn đồng) trong đó \(q\) (kg) là khối lượng sản phẩm sản xuất được. Xưởng chỉ sản xuất được tối đa 50 kg sản phẩm trong một tuần. a) Xưởng sản xuất càng nhiều thì lợi nhuận càng cao. b) Lợi nhuận lớn nhất khi xưởng sản xuất 26 kg sản phẩm trong một tuần. c) Sau khi sản xuất được 26 kg sản phẩm, càng sản xuất thêm thì lợi nhuận càng giảm. d) Lợi nhuận của xưởng thấp nhất khi không sản xuất.

Lập bảng biết thiên của hàm số hàm số \(P\left( q \right)\) trên đoạn \(\left[ {0;50} \right]\), xét tính đơn điệu, tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(P\left( q \right)\) trên đoạn \(\left[ {0;50} \right]\).

Xét hàm số \(P\left( q \right) = - {q^3} + 24{q^2} + 780q - 5000\) trên đoạn \(\left[ {0;50} \right]\).
Ta có:
\(P’\left( q \right) = - 3{q^2} + 48q + 780\)
\(P’\left( q \right) = 0 \Leftrightarrow q = 26\) hoặc \(q = - 0\) (loại)
Bảng biến thiên:
Advertisements (Quảng cáo)
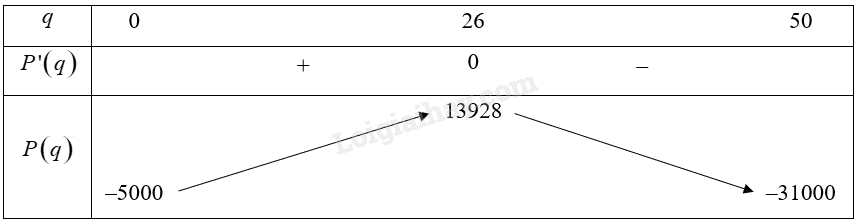
Vậy \(\mathop {\max }\limits_{\left[ {0;50} \right]} P\left( q \right) = P\left( {26} \right) = 13928,\mathop {\min }\limits_{\left[ {0;50} \right]} P\left( q \right) = P\left( {50} \right) = - 31000\).
Vậy lợi nhuận tăng khi sản xuất từ 0 đến 26 sản phẩm, lợi nhuận giảm khi sản xuất từ 26 đến 50 sản phẩm. Vậy a) sai, c) đúng.
Lợi nhuận lớn nhất khi xưởng sản xuất 26 kg sản phẩm trong một tuần. Vậy b) đúng.
Lợi nhuận của xưởng thấp nhất khi sản xuất 50 kg sản phẩm trong một tuần. Vậy d) sai.
a) S.
b) Đ.
c) Đ.
d) S.
