
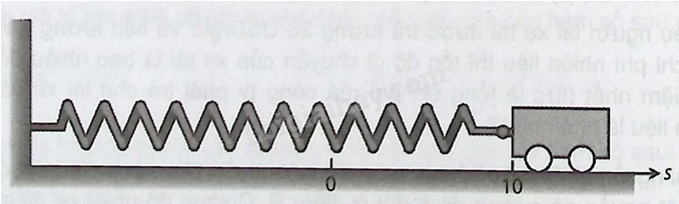
Một chiếc xe nhỏ chuyển động không có ma sát, gắn vào tường bằng một lò xo (xem hình vẽ), được kéo ra khỏi vị trí đứng yên \(10\) cm rồi thả ra tại thời điểm ban đầu \(t = 0\) giây để chuyển động trong \(4\) giây. Vị trí \(s\) (cm) tại thời điểm \(t\) giây là \(s = 10\cos \pi t\).
a) Tốc độ lớn nhất của xe là bao nhiêu? Khi nào xe chuyển động với tốc độ như vậy, khi đó xe đang ở vị trí nào và gia tốc lúc đó có độ lớn là bao nhiêu?
b) Xe ở đâu khi độ lớn gia tốc là lớn nhất? Khi đó vận tốc của xe là bao nhiêu?

Ý a: Xác định công thức vận tốc, gia tốc theo t. Tìm giá trị lớn nhất của tốc độ (lấy trị tuyệt đối vận tốc) trên đoạn bằng phương pháp đã học đồng thời tìm t. Thay các giá trị t vừa tìm được vào s để tìm được vị trí, thay vào a để tìm gia tốc. Giải thích trên thực tế xe đang ở vị trí nào khi đó.
Ý b: Tìm t để trị tuyệt đối gia tốc a lớn nhất, sau đó thay số để tìm s và v, từ đó giải thích trên thực tế vận tốc và vị trí của vật đang như thế nào.

a) Vận tốc của xe là \(v\left( t \right) = s’\left( t \right) = - 10\pi \sin \pi t\) (cm/s)
Advertisements (Quảng cáo)
Khi đó gia tốc của xe là \(a\left( t \right) = v’\left( t \right) = - 10{\pi ^2}\cos \pi t\) (cm/s2)
Ta có \(v’\left( t \right) = 0 \Leftrightarrow - 10{\pi ^2}\cos \pi t = 0 \Leftrightarrow \cos \pi t = 0 \Leftrightarrow \pi t = \frac{\pi }{2} + k2\pi ,k \in \mathbb{Z} \Leftrightarrow t = \frac{1}{2} + 2k,k \in \mathbb{Z}\)
Mà \(t \in \left[ {0;4} \right]\)nên ta tính được \(t \in \left\{ {\frac{1}{2};\frac{3}{2};\frac{5}{2};\frac{7}{2}} \right\}\).
Mặt khác, \(v\left( 0 \right) = v\left( 4 \right) = 0;v\left( {\frac{1}{2}} \right) = v\left( {\frac{3}{2}} \right) = v\left( {\frac{5}{2}} \right) = v\left( {\frac{7}{2}} \right) = - 10\pi \)
Tốc độ của xe là \(\left| {v\left( t \right)} \right|\), vậy tốc độ lớn nhất của xe là \(10\pi \) cm/s đạt được tại các thời điểm \(\frac{1}{2};\frac{3}{2};\frac{5}{2};\frac{7}{2}\) giây. Tại các thời điểm đó, xe đều có gia tốc bằng 0 và tại vị trí \(s = 0\) tức là ở vị trí xe đứng yên khi mà chưa kéo lò xo.
b) Ta có \(a’\left( t \right) = 10{\pi ^3}\sin \pi t\); \(a’\left( t \right) = 0 \Leftrightarrow 10{\pi ^3}\sin \pi t = 0 \Leftrightarrow t \in \left\{ {0;1;2;3;4} \right\}\)
Khi đó \(a\left( 0 \right) = a\left( 2 \right) = a\left( 4 \right) = - 10{\pi ^2};a\left( 1 \right) = a\left( 3 \right) = 10{\pi ^2}\).
Ta có \(\left| {a\left( t \right)} \right|\) là độ lớn của gia tốc do đó nó lớn nhất tại các thời điểm \(0;1;2;3;4\) giây.
Khi \(t = 0;2;4\) giây, xe ở vị trí \(s = 10\) cm; \(t = 1;3\) giây, xe ở vị trí \(s = - 10\) cm.
Vậy độ lớn gia tốc lớn nhất tại các vị trí \(s = 10\) cm hoặc \(s = - 10\) cm. (Tức là khi xe ở mép phải hoặc mép trái của quãng đường giao động) và tại các vị trí đó, vận tốc của xe đều bằng 0
