
Cho hàm số \(y = f\left( x \right) = \frac{{\sqrt {{x^2} + 3} }}{{x - 1}}\) có đồ thị như hình vẽ sau:
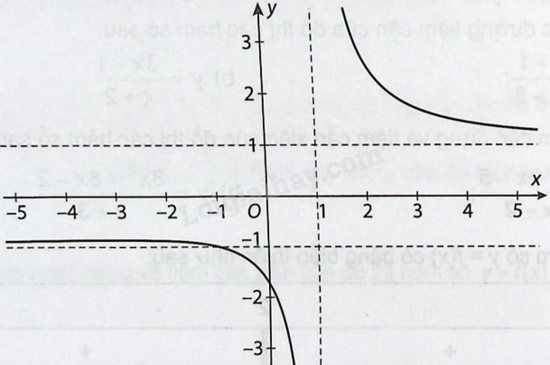
Hãy tìm các tiệm cận đứng và tiệm cận ngang của đồ thị hàm số đã cho.

Advertisements (Quảng cáo)
Tính cách giới hạn theo định nghĩa tiệm cận, quan sát hình vẽ để tìm ra tiệm cận.

Ta có \(\mathop {\lim }\limits_{x \to {1^ + }} y = \frac{{\sqrt {{x^2} + 3} }}{{x - 1}} = + \infty \); \(\mathop {\lim }\limits_{x \to {1^ - }} y = \frac{{\sqrt {{x^2} + 3} }}{{x - 1}} = - \infty \). Do đó đường thẳng \(x = 1\) là tiệm cận đứng của đồ thị hàm số.
\(\mathop {\lim }\limits_{x \to + \infty } y = \frac{{\sqrt {{x^2} + 3} }}{{x - 1}} = 1\). Do đó đường thẳng \(y = 1\) là tiệm cận ngang của đồ thị hàm số.
\(\mathop {\lim }\limits_{x \to - \infty } y = \frac{{\sqrt {{x^2} + 3} }}{{x - 1}} = - 1\). Do đó đường thẳng \(y = - 1\) là tiệm cận ngang của đồ thị hàm số
