Tìm giá trị lớn nhất, giá trị nhỏ nhất của các hàm số sau:
a) \(y = {x \over {4 + {x^2}}}\) trên khoảng \(( - \infty ; + \infty )\) ;
b) \(y = {1 \over {\cos x}}\) trên khoảng \(({\pi \over 2};{{3\pi } \over 2})\)
c) \(y = {1 \over {1 + {x^4}}}\) trên khoảng \(( - \infty ; + \infty )\) ;
d) \(y = {1 \over {\sin x}}\) trên khoảng \((0;\pi )\) .
Hướng dẫn làm bài:
a) \(y = {x \over {4 + {x^2}}}\) trên khoảng \(( - \infty ; + \infty )\)
\(\eqalign{
& y’ = {{4 - {x^2}} \over {{{(4 + {x^2})}^2}}} \cr
& y’ = 0 \Rightarrow \left[ \matrix{
x = - 2 \hfill \cr
x = 2 \hfill \cr} \right. \cr} \)
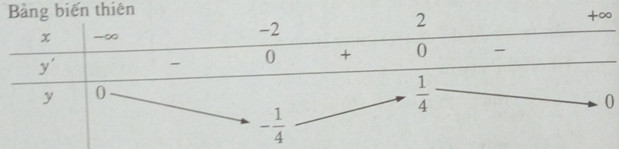
Từ đó ta có \(\mathop {\min }\limits_R f(x) = - {1 \over 4};\mathop {\max }\limits_R f(x) = {1 \over 4}\)
b) \(y = {1 \over {\cos x}}\) trên khoảng \(({\pi \over 2};{{3\pi } \over 2})\)
\(y’ = {{\sin x} \over {{{\cos }^2}x}};y’ = 0 < = > x = \pi\)
Bảng biến thiên:
Advertisements (Quảng cáo)
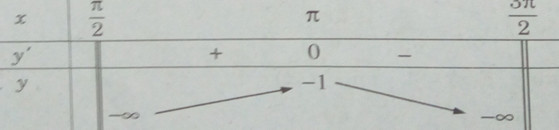
Hàm số không có giá trị nhỏ nhất. Giá trị lớn nhất của hàm số là: \(\mathop {\max }\limits_{({\pi \over 2};{{3\pi } \over 2})} y = y(\pi ) = - 1\)
c) \(y = {1 \over {1 + {x^4}}}\) trên khoảng \(( - \infty ; + \infty )\) ;
\(y’ = {{ - 4{x^3}} \over {{{(1 + {x^4})}^2}}};y’ = 0 < = > x = 0\)
Bảng biến thiên:
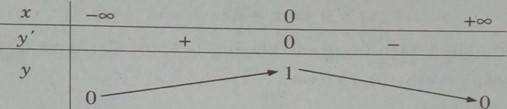
Hàm số không có giá trị nhỏ nhất. Giá trị lớn nhất là: \(\mathop {\max }\limits_R y = y(0) = 1\)
d) \(y = {1 \over {\sin x}}\) trên khoảng \((0;\pi )\)
\(y’ = {{ - \cos x} \over {{{\sin }^2}x}},y’ = 0 < = > x = {\pi \over 2}\)
Bảng biến thiên:
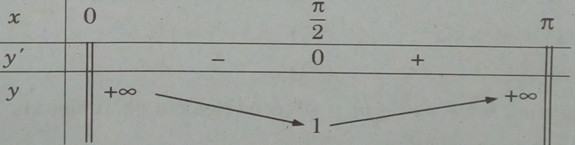
Hàm số không có giá trị lớn nhất. Giá trị nhỏ nhất của hàm số là: \(\mathop {\min }\limits_{(0;\pi )} y = y({\pi \over 2}) = 1\).
