Một hình nón tròn xoay có đỉnh là D, tâm của đường tròn đáy là O, đường sinh bằng l và có góc giữa đường sinh và mặt phẳng đáy bằng \(\alpha \).
a) Tính diện tích xung quanh của hình nón và thể tích khối nón được tạo nên.
b) Gọi I là một điểm trên đường cao DO của hình nón sao cho \({{DI} \over {DO}} = k(0 < k < l)\) . Tính diện tích thiết diện qua I và vuông góc với trục của hình nón.
Hướng dẫn làm bài:
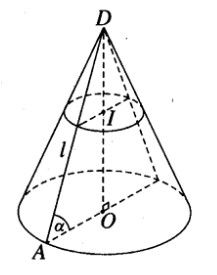
a) Gọi r là bán kính của đường tròn đáy.
Ta có \(OA{\rm{ }} = {\rm{ }}r{\rm{ }} = l.\cos \alpha \) (với O là tâm của đường tròn đáy và A là một điểm trên đường tròn đó).
Advertisements (Quảng cáo)
Ta suy ra: \({S_{xq}} = \pi rl = \pi {l^2}\cos \alpha \)
Khối nón có chiều cao \(h = DO = l\sin \alpha \) . Do đó thể tích V của khối nón được tính theo công thức \(V = {1 \over 3}Bh = {1 \over 3}\pi {r^2}.h\)
Vậy : \(V = {1 \over 3}\pi {l^2}{\cos ^2}\alpha .l\sin \alpha = {1 \over 3}\pi {l^3}{\cos ^2}\alpha \sin \alpha \)
b) Thiết diện qua I và vuông góc với trục hình nón là một hình tròn bán kính r’ với \({{r’} \over r} = {{DI} \over {DO}} = k\)
Gọi s là diện tích của thiết diện và S là diện tích của đáy hình tròn ta có:
\({s \over S} = {k^2}\Leftrightarrow s = {k^2}S\), trong đó \(S = \pi {r^2} = \pi {l^2}{\cos ^2}\alpha \)
Vậy diện tích của thiết diện đi qua điểm I và vuông góc với trục hình nón là: \(s = {k^2}S = {k^2}\pi {l^2}{\cos ^2}\alpha \)
