Cho S.ABC là hình chóp tam giác đều có các cạnh bên bằng a và có góc giữa các mặt bên và mặt phẳng đáy là \(\alpha \). Hình nón đỉnh S có đường tròn đáy nội tiếp tam giác đều ABC gọi là hình nón nội tiếp hình nón đã cho. Hãy tính diện tích xung quanh của hình nón này theo a và \(\alpha \) .
Hướng dẫn làm bài:
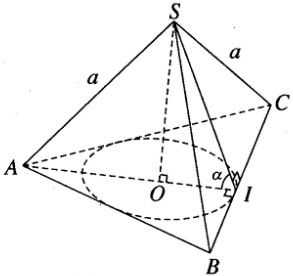
Gọi I là trung điểm của cạnh BC và O là tâm của tam giác đều ABC. Theo giả thiết ta có SA = SB = SC = a và \(\widehat {SIO} = \alpha \). Đặt OI = r, SO = h, ta có AO = 2r và
\(\left\{ {\matrix{{h = r\tan \alpha } \cr {{a^2} = {h^2} + 4{r^2}} \cr} } \right.\) (vì SA2 = SO2 + AO2 )
Advertisements (Quảng cáo)
Do đó \({a^2} = {r^2}{\tan ^2}\alpha + 4{r^2} = {r^2}({\tan ^2}\alpha + 4)\)
Vậy \(r = {a \over {\sqrt {{{\tan }^2}\alpha + 4} }}\)
Hình nón nội tiếp có đường sinh là : \(l = SI = {r \over {\cos \alpha }} = {a \over {\cos \alpha \sqrt {{{\tan }^2}\alpha + 4} }}\)
Diện tích xung quanh của hình nón nội tiếp hình chóp S.ABC là:
\({S_{xq}} = \pi rl = \pi .{a \over {\sqrt {{{\tan }^2}\alpha + 4} }}.{a \over {\cos \alpha \sqrt {{{\tan }^2}\alpha + 4} }} = {{\pi {a^2}} \over {\cos \alpha ({{\tan }^2}\alpha + 4)}}\)
