Câu hỏi 2 trang 35 SGK Hình học 12. Lời giải chi tiết Bài 1. Khái niệm về mặt tròn xoay
Cắt mặt xung quanh của một hình nón tròn xoay dọc theo một đường sinh rồi trải ra trên mặt phẳng ta được một nửa hình tròn bán kính R. Hỏi hình nón đó có bán kính r của đường tròn đáy và góc ở đỉnh của hình nón bằng bao nhiêu ?
Cắt mặt xung quanh của một hình nón tròn xoay dọc theo một đường sinh rồi trải ra trên mặt phẳng ta được một nửa hình tròn bán kính R ⇒ đường sinh có độ dài bằng R và chu vi đường tròn đáy bằng nửa chu vi đường tròn bán kính R.
Advertisements (Quảng cáo)
\( \Rightarrow r = {R \over 2}\)
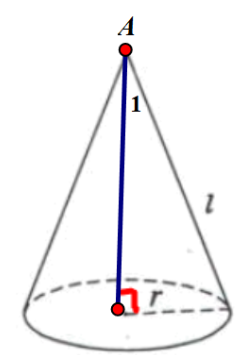
Ta có: \(\sin \widehat {{A_1}} = {r \over 1} = {r \over R} = {1 \over 2} \Rightarrow \widehat {{A_1}} = {30^0}\)
Suy ra, góc ở đỉnh hình chóp: \(\widehat A = 2\widehat {{A_1}} = {2.30^0} = {60^0}\)