Cho khối nón có bán kính đáy r = 12 cm và có góc ở đỉnh là \(\alpha = {120^0}\). Hãy tính diện tích của thiết diện đi qua hai đường sinh vuông góc với nhau.
Hướng dẫn làm bài:
Advertisements (Quảng cáo)
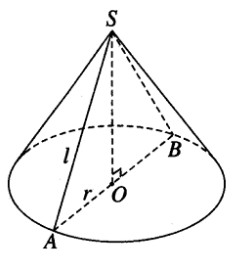
Theo giả thiết ta có góc ở đỉnh của hình nón là \(\widehat {ASB} = \alpha = {120^0}\). Gọi O là tâm của đường tròn đáy. Ta có: \(\widehat {ASO} = {60^0}\) và \(\sin {60^0} = {{OA} \over {SA}} = {r \over l}\) với l là độ dài đường sinh của hình nón.
Vậy \(l = {r \over {\sin {{60}^0}}} = {{12} \over {{{\sqrt 3 } \over 2}}} = {{24} \over {\sqrt 3 }}\)
Khi có hai đường sinh vuông góc với nhau ta có tam giác vuông có diện tích là \({1 \over 2}{l^2}\). Do đó, diện tích của thiết diện là: \(S = {1 \over 2}{l^2} = {1 \over 2}.{{{{24}^2}} \over 3} = 96(c{m^2})\).
