Cho mặt trụ xoay \((\Im )\) và một điểm S cố định nằm ngoài \((\Im )\) . Một đường thẳng d thay đổi luôn luôn đi qua S cắt \((\Im )\) tại A và B. Chứng minh rằng trung điểm I của đoạn thẳng AB luôn luôn nằm trên một mặt trụ xác định.
Hướng dẫn làm bài:
Advertisements (Quảng cáo)
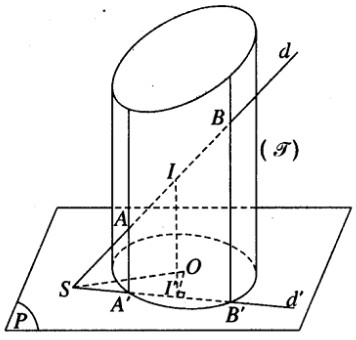
Gọi (P) là mặt phẳng đi qua S và vuông góc với trục của mặt trụ \((\Im )\). Mặt phẳng (P) cắt \((\Im )\) theo một đường tròn tâm O. Ta hãy xét một vị trí của đường thẳng d. Gọi A, B là giao điểm của d với \((\Im )\) và I là trung điểm của đoạn AB. Chiếu A, B, I theo phương vuông góc với mặt phẳng (P) ta được các điểm theo thứ tự là A’ , B’ , I’ thẳng hàng với S, trong đó A’, B’ nằm trên đường tròn tâm O trong mặt phẳng (P) và I’ là trung điểm của đoạn A’B’. Do đó điểm I’ luôn luôn nằm trên đường tròn đường kính SO trong mặt phẳng (P) và đường thẳng II’ vuông góc với (P). Ta suy ra đường thẳng II’ nằm trên mặt trụ \((\Im ‘)\) chứa đường tròn đường kính SO nằm trong (P) và có trục song song với trục của mặt trụ \((\Im )\) .
Tất nhiên, điểm I chỉ nằm trong phần mặt trụ \((\Im ‘)\) thuộc miền trong của mặt trụ \((\Im )\)
