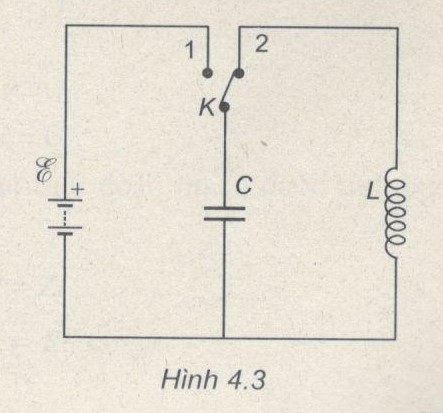
Cho mạch điện như ở hình 4.3: \(C = 500pF;L = 0,2mH;\xi = 1,5V;\) lấy \({\pi ^2} \approx 10\). Tại thời điểm t = 0, khóa K chuyển từ (1) sang (2). Thiết lập công thức biểu diễn sự phụ thuộc của điện tích trên tụ điện C vào thời gian
Giải
Khi K ở vị trí 1 (Hình 4.3), tụ C có điện tích:
\({q_0} = C\xi= 7,{5.10^{ - 10}}\,\,C\)
Khi K chuyển sang vị trí 2 thì trên mạch LC có dao động điện với tần số góc:
\(\omega = {1 \over {\sqrt {LC} }} \approx \sqrt {10} {.10^6} \approx {10^6}\pi \,\,rad/s\)
Advertisements (Quảng cáo)
Công thức xác định điện tích q trên trụ C ở thời điểm t có dạng:
\(q = {q_0}\cos \left( {\omega t + \varphi } \right) = {q_0}\cos \left( {{{10}^6}\pi t + \varphi } \right)\)
Ở thời điểm t = 0, q có giá trị cực đại \({q_{\max }} = {q_0}\), nghĩa là:
\({q_0}\cos \varphi = {q_0} \Rightarrow \varphi = 0\)
Từ đó ta có:
\(q = 7,{5.10^{ - 10}}\cos \left( {{{10}^6}\pi t} \right)\,\,\left( C \right)\)
