Advertisements (Quảng cáo)
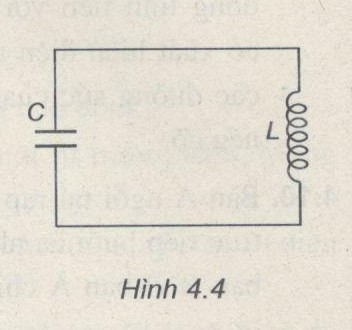
Một mạch dao động gồm một tụ điện có điện dung C = 25 pF và và một cuộn cảm thuần có hệ số tự cảm \(L = {10^{ – 4}}H\)(Hình 4.4). Giả sử ở thời điểm ban đầu cường độ dòng điện đạt cực đại bằng 40 mA. Tìm công thức xác định cường độ dòng điện, công thức xác định điện tích trên các bản tụ và hiệu điện thế giữa hai bản tụ điện.
Giải
Trong mạch dao động LC, điện tích q của tụ điện, cường độ dòng điện i đều biến thiên điều hòa với tần số góc: \(\omega = {1 \over {\sqrt {LC} }} = {2.10^7}\,rad/s\)
Theo đề bài: \(t = 0,\,i = {I_0} = 40\,mA.\)
Ta có: \(\omega = {1 \over {\sqrt {LC} }} = {2.10^7}\pi \,\,rad/s;\,{I_0} = {q_0}\omega \). Từ đó suy ra:
\({q_0} = {{{I_0}} \over \omega } = {2.10^{ – 9}}\,\,C\)
Advertisements (Quảng cáo)
Công thức xác định cường độ dòng điện: \(i = 40\cos \left( {{{2.10}^7}t} \right)\,\,\left( {mA} \right)\)
Công thức xác định điện tích trên các bản tụ điện:
\(q = {2.10^{ – 9}}\cos \left( {{{2.10}^7}t – {\pi \over 2}} \right)\,\,\left( C \right)\)
Công thức xác định hiệu điện thế giữa hai bản tụ:
\(u = {q \over C} = 80\cos \left( {{{2.10}^7}t – {\pi \over 2}} \right)\,\,\left( V \right)\)