
Trong một nhà hàng, mỗi tuần để chế biến x phần ăn (x lấy giá trị trong khoảng từ 30 đến 120) thì chi phí trung bình (đơn vị: nghìn đồng) của một phần ăn được cho bởi công thức:
\(\overline C (x) = 2x - 230 + \frac{{7200}}{x}\)
a) Khảo sát và vẽ đồ thị hàm số \(\overline C (x)\) trên [30; 120].
b) Từ kết quả trên, tìm số phần ăn sao cho chi phí trung bình của một phần ăn là thấp nhất.

a) Bước 1. Tìm tập xác định của hàm số
Bước 2. Xét sự biến thiên của hàm số
− Tìm đạo hàm y’, xét dấu y’, xác định khoảng đơn điệu, cực trị (nếu có) của hàm số.
− Tìm giới hạn tại vô cực, giới hạn vô cực của hàm số và các đường tiệm cận của đồ thị hàm số (nếu có).
− Lập bảng biến thiên của hàm số.
Bước 3. Vẽ đồ thị của hàm số
− Xác định các điểm cực trị (nếu có), giao điểm của đồ thị với các trục toạ độ (nếu có và dễ tìm), ...
− Vẽ các đường tiệm cận của đồ thị hàm số (nếu có).
Advertisements (Quảng cáo)
− Vẽ đồ thị hàm số.
b) Quan sát bảng biến thiên

Tập xác định: \(D = [30;120]\)
- Chiều biến thiên:
\(\overline C ‘(x) = 2 - \frac{{7200}}{{{x^2}}} = 0 \Leftrightarrow \left[ \begin{array}{l}x = - 60(loai)\\x = 60\end{array} \right.\)
Trên các khoảng (30; 60) thì y’ < 0 nên hàm số nghịch biến trên khoảng đó. Trên khoảng (60; 120) thì y’ > 0 nên hàm số đồng biến trên khoảng đó.
- Cực trị:
Hàm số đạt cực đại tại x = 60 và \({y_{cd}} = 10\)
- Các giới hạn tại vô cực:
\(\mathop {\lim }\limits_{x \to - \infty } \overline C (x) = \mathop {\lim }\limits_{x \to - \infty } (2x - 230 + \frac{{7200}}{x}) = - \infty \); \(\mathop {\lim }\limits_{x \to + \infty } \overline C (x) = \mathop {\lim }\limits_{x \to + \infty } (2x - 230 + \frac{{7200}}{x}) = + \infty \)
- Bảng biến thiên:
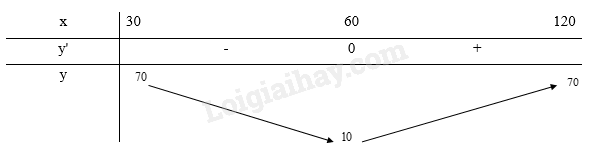
Đồ thị hàm số:
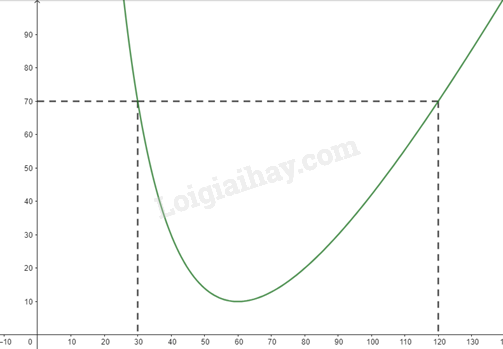
b) Từ bảng biến thiên, ta thấy \(\mathop {\min }\limits_{[30;120]} \overline C (x) = \overline C (60) = 10\)
Vậy để chi phí trung bình của một phần ăn là thấp nhất thì số phần ăn là 10
