
Cho hàm số bậc ba y = f(x) có đồ thị như Hình 3. Viết công thức của hàm số
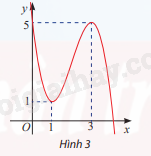

Xác định các cực trị của đồ thị hàm số và giao điểm của đồ thị hàm số với các trục tọa độ

Hàm số có dạng: \(y = a{x^3} + b{x^2} + cx + d(a < 0)\)
Advertisements (Quảng cáo)
Đồ thị hàm số giao với Oy tại điểm (0; 5) nên: \(y(0) = a{.0^3} + b{.0^2} + c.0 + d = 5 \Leftrightarrow d = 5\)
Đồ thị hàm số đi qua điểm (3; 5) nên: \(y = a{.3^3} + b{.3^2} + c.3 + 5 = 5 \Leftrightarrow 27a + 9b + 3c = 0\)
Đồ thị hàm số đi qua điểm (1; 1) nên: \(y(1) = a{.1^3} + b{.1^2} + c.1 + 5 = 1 \Leftrightarrow a + b + c = - 4\)
Ta có: \(y’ = 3a{x^2} + 2bx + c\)
Hàm số đạt cực đại tại điểm (3; 5) nên: \(y'(3) = 3a{x^2} + 2bx + c = 3.a{.3^2} + 2.b.3 + c = 0\)\( \Leftrightarrow 27a + 6b + c = 0\)
Ta có hệ phương trình: \(\left\{ \begin{array}{l}27a + 9b + 3c = 0\\a + b + c = - 4\\27a + 6b + c = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = - 1\\b = 6\\c = - 9\end{array} \right.\)
Vậy hàm số là \(y = - {x^3} + 6{x^2} - 9x + 5\)
