Khám phá2
Trả lời câu hỏi Khám phá 2 trang 70
Kết quả điều tra tổng thu nhập trong năm 2022 của một số hộ gia đình trong một địa phương được ghi lại ở bảng sau:
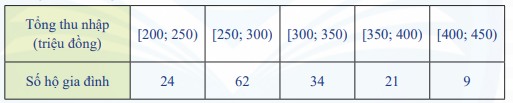
a) Hãy tìm các tứ phân vị \({Q_1}\) và \({Q_3}\).
b) Một doanh nghiệp địa phương muốn hướng dịch vụ của mình đến các gia đình có mức thu nhập ở tầm trung, tức là 50% các hộ gia đình có mức thu nhập ở chính giữa so với tất cả các hộ gia đình của địa phương. Hỏi doanh nghiệp cần hướng đến các gia đình có mức thu nhập trong khoảng nào?

Tứ phân vị thứ k, kí hiệu là \({Q_k}\), với k = 1, 2, 3 của mẫu số liệu ghép nhóm được xác định như sau:
\({Q_k} = {u_m} + \frac{{\frac{{kn}}{4} - C}}{{{n_m}}}({u_{m + 1}} - {u_m})\)
trong đó:
\(n = {n_1} + {n_2} + {n_3} + ... + {n_k}\) là cỡ mẫu
\([{u_m};{u_{m + 1}}]\) là nhóm chứa tứ phân vị thứ k
\({n_m}\) là tần số của nhóm chứa tứ phân vị thứ k
\(C = {n_1} + {n_2} + {n_3} + ... + {n_{m - 1}}\)

a) Cỡ mẫu n = 150
Gọi \({x_1};{\rm{ }}{x_2}; \ldots ;{\rm{ }}{x_{150}}\) là mẫu số liệu gốc gồm thu nhập của 150 hộ gia đình được xếp theo thứ tự không giảm.
Ta có: \({x_1};{\rm{ }}{x_2}; \ldots ;{\rm{ }}{x_{24}} \in [200;250)\); \({x_{25}}; \ldots ;{\rm{ }}{x_{86}} \in [250;300)\); \({x_{87}}; \ldots ;{\rm{ }}{x_{120}} \in [300;350)\); \({x_{121}}; \ldots ;{\rm{ }}{x_{141}} \in [350;400)\); \({x_{142}}; \ldots ;{\rm{ }}{x_{150}} \in [400;450)\)
Tứ phân vị thứ nhất của mẫu số liệu gốc là \({x_{38}} \in [250;300)\). Do đó, tứ phân vị thứ nhất của mẫu số liệu ghép nhóm là: \({Q_1} = 250 + \frac{{\frac{{150}}{4} - 24}}{{62}}(300 - 250) = \frac{{16175}}{{62}}\)
Tứ phân vị thứ ba của mẫu số liệu gốc là \({x_{113}} \in [300;350)\). Do đó, tứ phân vị thứ ba của mẫu số liệu ghép nhóm là: \({Q_3} = 300 + \frac{{\frac{{3.150}}{4} - (24 + 62)}}{{34}}(350 - 300) = \frac{{11525}}{{34}}\)
b) Doanh nghiệp cần hướng đến các gia đình có mức thu nhập trong khoảng \([{Q_1};{Q_3}) = [260,89;338,97)\)(triệu đồng)
Thực hành2
Trả lời câu hỏi Thực hành 2 trang 71
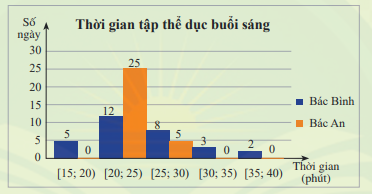
Hãy so sánh khoảng tứ phân vị của mẫu số liệu ghép nhóm về thời gian tập thể dục buổi sáng mỗi ngày của bác Bình và bác An trong Khởi động.

Khoảng tứ phân vị của mẫu số liệu ghép nhóm, kí hiệu \({\Delta _Q}\), là hiệu giữa tứ phân vị thứ ba \({Q_3}\) và tứ phân vị thứ nhất \({Q_1}\) của mẫu số liệu ghép nhóm đó, tức là \({\Delta _Q} = {Q_3} - {Q_1}\).

Cỡ mẫu \(n = 30\);
Gọi \({x_1};{\rm{ }}{x_2}; \ldots ;{\rm{ }}{x_{30}}\) là mẫu số liệu gốc về thời gian tập thể dục buổi sáng mỗi ngày của bác An được xếp theo thứ tự không giảm.
Ta có: \({x_1};{\rm{ }}{x_2}; \ldots ;{\rm{ }}{x_{25}} \in [20;25)\); \({x_{26}}; \ldots ;{\rm{ }}{x_{30}} \in [25;30)\);
Tứ phân vị thứ nhất của mẫu số liệu gốc là \({x_8} \in [20;25)\). Do đó, tứ phân vị thứ nhất của mẫu số liệu ghép nhóm là: \({Q_1} = 20 + \frac{{\frac{{30}}{4}}}{{25}}(25 - 20) = \frac{{43}}{2}\)
Tứ phân vị thứ ba của mẫu số liệu gốc là \({x_{23}} \in [20;25)\). Do đó, tứ phân vị thứ ba của mẫu số liệu ghép nhóm là: \({Q_3} = 20 + \frac{{\frac{{3.30}}{4}}}{{25}}(25 - 20) = \frac{{49}}{2}\)
Khoảng tứ phân vị của mẫu số liệu ghép nhóm là: \({\Delta _Q} = {Q_3} - {Q_1} = 3\)
Gọi \({y_1};{\rm{ }}{y_2}; \ldots ;{\rm{ }}{y_{30}}\) là mẫu số liệu gốc về thời gian tập thể dục buổi sáng mỗi ngày của bác Bình được xếp theo thứ tự không giảm.
Ta có: \({y_1};{\rm{ }}{y_2}; \ldots ;{\rm{ }}{y_5} \in [15;20)\); \({y_6}; \ldots ;{\rm{ }}{y_{17}} \in [20;25)\);\({y_{18}}; \ldots ;{\rm{ }}{y_{25}} \in [25;30)\);\({y_{26}};{y_{27}};{\rm{ }}{y_{28}} \in [30;35)\);\({y_{29}};{y_{30}} \in [35;40)\)
Tứ phân vị thứ nhất của mẫu số liệu gốc là \({y_8} \in [20;25)\). Do đó, tứ phân vị thứ nhất của mẫu số liệu ghép nhóm là: \({Q_1}’ = 20 + \frac{{\frac{{30}}{4}}}{{12}}(25 - 20) = \frac{{185}}{8}\)
Tứ phân vị thứ ba của mẫu số liệu gốc là \({y_{23}} \in [25;30)\). Do đó, tứ phân vị thứ ba của mẫu số liệu ghép nhóm là: \({Q_3}’ = 25 + \frac{{\frac{{3.30}}{4} - (5 + 12)}}{8}(30 - 25) = \frac{{455}}{{16}}\)
Khoảng tứ phân vị của mẫu số liệu ghép nhóm là: \({\Delta _Q}’ = {Q_3}’ - {Q_1}’ = \frac{{85}}{{16}}\)
Vậy khoảng tứ phân vị của mẫu số liệu ghép nhóm về thời gian tập thể dục buổi sáng mỗi ngày của bác Bình lớn hơn bác An
Thực hành3
Trả lời câu hỏi Thực hành 3 trang 72
a) Hãy tìm khoảng biến thiên và khoảng tứ phân vị của mẫu số liệu ghép nhóm ở Ví dụ 4 sau khi đã loại bỏ các giá trị ngoại lệ. Em có nhận xét gì về khoảng biến thiên, khoảng tứ phân vị vừa tìm được và khoảng biến thiên, khoảng tứ phân vị ban đầu?
Hằng ngày ông Thắng đều đi xe buýt từ nhà đến cơ quan. Dưới đây là bảng thống kê thời gian của 100 lần ông Thắng đi xe buýt từ nhà đến cơ quan.

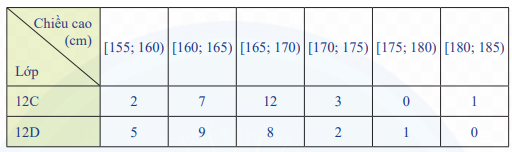
b) Hãy so sánh độ phân tán của nửa giữa hai mẫu số liệu chiều cao của các học sinh nữ lớp 12C và 12D ở Thực hành 1.

a) Giá trị x trong mẫu số liệu là giá trị ngoại lệ nếu \(x > {Q_3} + 1,5{\Delta _Q}\) hoặc \(x < {Q_1} - 1,5{\Delta _Q}\)
Khoảng biến thiên của mẫu số liệu ghép nhóm là hiệu số giữa đầu mút phải của nhóm cuối cùng và đầu mút trái của nhóm đầu tiên có chứa dữ liệu của mẫu số liệu.
Tứ phân vị thứ k, kí hiệu là \({Q_k}\), với k = 1, 2, 3 của mẫu số liệu ghép nhóm được xác định như sau:
\({Q_k} = {u_m} + \frac{{\frac{{kn}}{4} - C}}{{{n_m}}}({u_{m + 1}} - {u_m})\)
trong đó:
\(n = {n_1} + {n_2} + {n_3} + ... + {n_k}\) là cỡ mẫu
\([{u_m};{u_{m + 1}}]\) là nhóm chứa tứ phân vị thứ k
\({n_m}\) là tần số của nhóm chứa tứ phân vị thứ k
\(C = {n_1} + {n_2} + {n_3} + ... + {n_{m - 1}}\)
Khoảng tứ phân vị của mẫu số liệu ghép nhóm, kí hiệu \({\Delta _Q}\), là hiệu giữa tứ phân vị thứ ba \({Q_3}\) và tứ phân vị thứ nhất \({Q_1}\) của mẫu số liệu ghép nhóm đó, tức là \({\Delta _Q} = {Q_3} - {Q_1}\).
b) Tìm khoảng tứ phân vị của 2 nhóm số liệu rồi so sánh

Advertisements (Quảng cáo)
a) Gọi \({x_1};{\rm{ }}{x_2}; \ldots ;{\rm{ }}{x_{100}}\) là mẫu số liệu gốc gồm thời gian 100 lần ông Thắng đi xe buýt từ nhà đến cơ quan được xếp theo thứ tự không giảm.
Khoảng biến thiên R = 33 – 15 = 18(phút)
Ta có: \({x_1};{\rm{ }}{x_2}; \ldots ;{\rm{ }}{x_{22}} \in [15;18)\); \({x_{23}}; \ldots ;{\rm{ }}{x_{60}} \in [18;21)\); \({x_{61}}; \ldots ;{\rm{ }}{x_{87}} \in [21;24)\); \({x_{88}}; \ldots ;{\rm{ }}{x_{95}} \in [24;27)\);\({x_{96}}; \ldots ;{\rm{ }}{x_{99}} \in [27;30)\);\({x_{100}} \in [30;33)\)
Tứ phân vị thứ nhất của mẫu số liệu gốc là \(\frac{1}{2}({x_{25}} + {x_{26}}) \in [18;21)\). Do đó, tứ phân vị thứ nhất của mẫu số liệu ghép nhóm là: \({Q_1} = 18 + \frac{{\frac{{100}}{4} - 22}}{{38}}(21 - 18) = \frac{{693}}{{38}}\)
Tứ phân vị thứ ba của mẫu số liệu gốc là \(\frac{1}{2}({x_{75}} + {x_{76}}) \in [21;24)\). Do đó, tứ phân vị thứ ba của mẫu số liệu ghép nhóm là: \({Q_3} = 21 + \frac{{\frac{{3.100}}{4} - (22 + 38)}}{{27}}(24 - 21) = \frac{{68}}{3}\)
Khoảng tứ phân vị của mẫu số liệu ghép nhóm là: \({\Delta _Q} = {Q_3} - {Q_1} = \frac{{505}}{{114}}\)
Giá trị x trong mẫu số liệu là giá trị ngoại lệ nếu \(x > {Q_3} + 1,5{\Delta _Q}\) hoặc \(x < {Q_1} - 1,5{\Delta _Q}\)
Hay \(x > \frac{{39}}{2} + 1,5.\frac{{24}}{{19}} = 21,39\) hoặc \(x < \frac{{693}}{{38}} - 1,5.\frac{{24}}{{19}} = 16,34\)
Vậy các giá trị ngoại lệ thuộc khoảng [15;18); [24;27); [27;30); [30;33)
Khoảng biến thiên của mẫu số liệu ghép nhóm sau khi loại bỏ giá trị ngoại lệ: 24 – 18 = 6(phút)
Gọi \({z_1};{\rm{ }}{z_2}; \ldots ;{\rm{ }}{z_{65}}\) là mẫu số liệu gốc gồm thời gian 65 lần ông Thắng đi xe buýt từ nhà đến cơ quan được xếp theo thứ tự không giảm, sau khi đã loại bỏ các giá trị ngoại lệ
Ta có: \({z_1};{\rm{ }}{z_2}; \ldots ;{\rm{ }}{z_{38}} \in [18;21)\); \({z_{39}}; \ldots ;{\rm{ }}{x_{65}} \in [21;24)\)
Tứ phân vị thứ nhất của mẫu số liệu gốc là \({z_{17}} \in [18;21)\). Do đó, tứ phân vị thứ nhất của mẫu số liệu ghép nhóm là: \({Q_1}” = 18 + \frac{{\frac{{65}}{4}}}{{38}}(21 - 18) = \frac{{2931}}{{152}}\)
Tứ phân vị thứ ba của mẫu số liệu gốc là \({z_{50}} \in [21;24)\). Do đó, tứ phân vị thứ ba của mẫu số liệu ghép nhóm là: \({Q_3}” = 21 + \frac{{\frac{{3.65}}{4} - 38}}{{27}}(24 - 21) = \frac{{799}}{{36}}\)
Khoảng tứ phân vị của mẫu số liệu ghép nhóm là: \({\Delta _Q}” = {Q_3}” - {Q_1}” = 2,91\)
Nhận xét: Sau khi loại bỏ giá trị ngoại lệ, khoảng biến thiên mới giảm mạnh còn khoảng tứ phân vị mới không bị ảnh hưởng nhiều
b) Cỡ mẫu \(n = 25\)
Gọi \({x_1};{\rm{ }}{x_2}; \ldots ;{\rm{ }}{x_{25}}\) là mẫu số liệu gốc về chiều cao của các bạn học sinh nữ lớp 12C được xếp theo thứ tự không giảm.
Ta có: \({x_1};{\rm{ }}{x_2} \in [155;160)\); \({x_3}; \ldots ;{\rm{ }}{x_9} \in [160;165)\);\({x_{10}}; \ldots ;{\rm{ }}{x_{21}} \in [165;170)\);\({x_{22}}; \ldots ;{\rm{ }}{x_{24}} \in [170;175)\);\({x_{25}} \in [180;185)\)
Tứ phân vị thứ nhất của mẫu số liệu gốc là \(\frac{1}{2}({x_6} + {x_7}) \in [160;165)\). Do đó, tứ phân vị thứ nhất của mẫu số liệu ghép nhóm là: \({Q_1} = 160 + \frac{{\frac{{25}}{4} - 2}}{7}(165 - 160) = \frac{{4565}}{{28}}\)
Tứ phân vị thứ ba của mẫu số liệu gốc là \({x_{19}} \in [165;170)\). Do đó, tứ phân vị thứ ba của mẫu số liệu ghép nhóm là: \({Q_3} = 165 + \frac{{\frac{{3.25}}{4} - (2 + 7)}}{{12}}(170 - 165) = \frac{{2705}}{{16}}\)
Khoảng tứ phân vị của mẫu số liệu ghép nhóm là: \({\Delta _Q} = {Q_3} - {Q_1} = \frac{{675}}{{112}}\)
Gọi \({y_1};{\rm{ }}{y_2}; \ldots ;{\rm{ }}{y_{25}}\) là mẫu số liệu gốc về chiều cao của các bạn học sinh nữ lớp 12D được xếp theo thứ tự không giảm.
Ta có: \({y_1};{\rm{ }}{y_2}; \ldots ;{\rm{ }}{y_5} \in [155;160)\); \({y_6}; \ldots ;{\rm{ }}{y_{14}} \in [160;165)\);\({y_{15}}; \ldots ;{\rm{ }}{y_{22}} \in [165;170)\);\({y_{23}};{\rm{ }}{{\rm{y}}_{24}} \in [170;175)\);\({y_{25}} \in [175;180)\)
Tứ phân vị thứ nhất của mẫu số liệu gốc là \(\frac{1}{2}({y_6} + {y_7}) \in [160;165)\). Do đó, tứ phân vị thứ nhất của mẫu số liệu ghép nhóm là: \({Q_1}’ = 160 + \frac{{\frac{{25}}{4} - 5}}{9}(165 - 160) = \frac{{5785}}{{36}}\)
Tứ phân vị thứ ba của mẫu số liệu gốc là \({y_{19}} \in [165;170)\). Do đó, tứ phân vị thứ ba của mẫu số liệu ghép nhóm là: \({Q_3}’ = 165 + \frac{{\frac{{3.25}}{4} - (5 + 9)}}{8}(170 - 165) = \frac{{5375}}{{32}}\)
Khoảng tứ phân vị của mẫu số liệu ghép nhóm là: \({\Delta _Q}’ = {Q_3}’ - {Q_1}’ = \frac{{2095}}{{288}}\)
Có \({\Delta _Q}’ > {\Delta _Q}\) nên chiều cao của các bạn học sinh nữ lớp 12D có độ phân tán lơn hơn lớp 12C
Vận dụng
Trả lời câu hỏi Vận dụng trang 73
Giả sử kết quả khảo sát hai khu vực A và B về độ tuổi kết hôn của một số phụ nữ vừa lập gia đình được cho ở bảng sau:

a) Hãy tìm khoảng biến thiên và khoảng tứ phân vị của từng mẫu số liệu ghép nhóm ứng với mỗi khu vực A và B.
b) Nếu so sánh theo khoảng tứ phân vị thì phụ nữ ở khu vực nào có độ tuổi kết hôn đồng đều hơn?

a) Khoảng biến thiên của mẫu số liệu ghép nhóm là hiệu số giữa đầu mút phải của nhóm cuối cùng và đầu mút trái của nhóm đầu tiên có chứa dữ liệu của mẫu số liệu.
Tứ phân vị thứ k, kí hiệu là \({Q_k}\), với k = 1, 2, 3 của mẫu số liệu ghép nhóm được xác định như sau:
\({Q_k} = {u_m} + \frac{{\frac{{kn}}{4} - C}}{{{n_m}}}({u_{m + 1}} - {u_m})\)
trong đó:
\(n = {n_1} + {n_2} + {n_3} + ... + {n_k}\) là cỡ mẫu
\([{u_m};{u_{m + 1}}]\) là nhóm chứa tứ phân vị thứ k
\({n_m}\) là tần số của nhóm chứa tứ phân vị thứ k
\(C = {n_1} + {n_2} + {n_3} + ... + {n_{m - 1}}\)
Khoảng tứ phân vị của mẫu số liệu ghép nhóm, kí hiệu \({\Delta _Q}\), là hiệu giữa tứ phân vị thứ ba \({Q_3}\) và tứ phân vị thứ nhất \({Q_1}\) của mẫu số liệu ghép nhóm đó, tức là \({\Delta _Q} = {Q_3} - {Q_1}\).
b) Khoảng tứ phân vị càng bé thì dữ liệu càng tập trung xung quanh trung vị

Khoảng biến thiên của mẫu số liệu ghép nhóm ứng với khu vực A là: 34 – 19 = 15(tuổi)
Khoảng biến thiên của mẫu số liệu ghép nhóm ứng với khu vực B là: 31 – 19 = 12(tuổi)
Cỡ mẫu \(n = 100\)
Gọi \({x_1};{\rm{ }}{x_2}; \ldots ;{\rm{ }}{x_{100}}\) là mẫu số liệu gốc về độ tuổi kết hôn của phụ nữ ở khu vực A được xếp theo thứ tự không giảm.
Ta có: \({x_1};{\rm{ }}{x_2}; \ldots ;{\rm{ }}{x_{10}} \in [19;22)\); \({x_{11}}; \ldots ;{\rm{ }}{x_{37}} \in [22;25)\);\({x_{38}}; \ldots ;{\rm{ }}{x_{68}} \in [25;28)\);\({x_{69}}; \ldots ;{\rm{ }}{x_{93}} \in [28;31)\);\({x_{94}}; \ldots ;{\rm{ }}{x_{100}} \in [31;34)\)
Tứ phân vị thứ nhất của mẫu số liệu gốc là \(\frac{1}{2}({x_{25}} + {x_{26}}) \in [22;25)\). Do đó, tứ phân vị thứ nhất của mẫu số liệu ghép nhóm là: \({Q_1} = 22 + \frac{{\frac{{100}}{4} - 10}}{{27}}(25 - 22) = \frac{{71}}{3}\)
Tứ phân vị thứ ba của mẫu số liệu gốc là \(\frac{1}{2}({x_{75}} + {x_{76}}) \in [28;31)\). Do đó, tứ phân vị thứ ba của mẫu số liệu ghép nhóm là: \({Q_3} = 28 + \frac{{\frac{{3.100}}{4} - (10 + 27 + 31)}}{{25}}(31 - 28) = \frac{{721}}{{25}}\)
Khoảng tứ phân vị của mẫu số liệu ghép nhóm là: \({\Delta _Q} = {Q_3} - {Q_1} = \frac{{388}}{{75}}\)
Gọi \({y_1};{\rm{ }}{y_2}; \ldots ;{\rm{ }}{y_{100}}\) là mẫu số liệu gốc về độ tuổi kết hôn của phụ nữ ở khu vực B được xếp theo thứ tự không giảm.
Ta có: \({y_1};{\rm{ }}{y_2}; \ldots ;{\rm{ }}{y_{47}} \in [19;22)\); \({y_{48}}; \ldots ;{\rm{ }}{y_{87}} \in [22;25)\);\({y_{88}}; \ldots ;{\rm{ }}{y_{98}} \in [25;30)\);\({y_{99}};{y_{100}} \in [28;31)\)
Tứ phân vị thứ nhất của mẫu số liệu gốc là \(\frac{1}{2}({y_{25}} + {y_{26}}) \in [19;22)\). Do đó, tứ phân vị thứ nhất của mẫu số liệu ghép nhóm là: \({Q_1}’ = 19 + \frac{{\frac{{100}}{4}}}{{47}}(22 - 19) = \frac{{968}}{{47}}\)
Tứ phân vị thứ ba của mẫu số liệu gốc là \(\frac{1}{2}({y_{75}} + {y_{76}}) \in [22;25)\). Do đó, tứ phân vị thứ ba của mẫu số liệu ghép nhóm là: \({Q_3}’ = 22 + \frac{{\frac{{3.100}}{4} - 47}}{{40}}(25 - 22) = \frac{{241}}{{10}}\)
Khoảng tứ phân vị của mẫu số liệu ghép nhóm là: \({\Delta _Q}’ = {Q_3}’ - {Q_1}’ = \frac{{1647}}{{470}}\)
b) Có \({\Delta _Q}’ < {\Delta _Q}\) nên phụ nữ ở khu vực B có độ tuổi kết hôn đồng đều hơn
