Câu hỏi/bài tập:

Người ta cần rào một mảnh đất hình chữ nhật ABCD có diện tích là 600 m². Trên mảnh đất này, người ta chia làm ba miếng đất hình chữ nhật có diện tích bằng nhau (Hình 1.40). Giá tiền để xây dựng hàng rào bên trong và bao bên ngoài là 60.000 đồng mỗi mét, biết rằng chiều dài hình chữ nhật ABCD không vượt quá 60 m. Tìm chiều dài và chiều rộng của hình chữ nhật ABCD sao cho chi phí xây dựng hàng rào là thấp nhất (làm tròn kết quả đến hàng phần trăm).
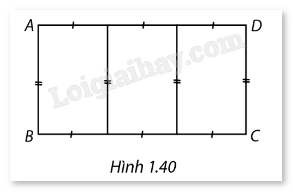

- Đặt chiều dài là ? và chiều rộng là ? của hình chữ nhật ABCD.
- Tính chi phí xây dựng hàng rào dựa trên chiều dài và chiều rộng.
- Viết hàm chi phí cần tối ưu và điều kiện ràng buộc.
- Sử dụng đạo hàm để tìm giá trị tối ưu.

Gọi chiều dài là \(x\) \((0 < x \le 60)\) và chiều rộng là \(y\) \((0 < y \le x)\) của hình chữ nhật ABCD.
Diện tích của hình chữ nhật ABCD là: \(xy = 600\)
- Chi phí hàng rào ngoài là 2x+2y.
- Chi phí hàng rào bên trong là 2y.
-Tổng chi phí là: \(C = 60.000 \times (2x + 4y)\)
Viết hàm mục tiêu:
Advertisements (Quảng cáo)
\(C = 60.000 \times \left( {2x + 4 \cdot \frac{{600}}{x}} \right) = 120.000 \times \left( {x + \frac{{1200}}{x}} \right)\)
Tìm giá trị cực trị: \(f(x) = x + \frac{{1200}}{x}\)
- Tính đạo hàm: \(f'(x) = 1 - \frac{{1200}}{{{x^2}}}\)
- Cho đạo hàm bằng 0: \(1 - \frac{{1200}}{{{x^2}}} = 0 \Rightarrow {x^2} = 1200 \Rightarrow x = \sqrt {1200} \approx 34,64(\;{\rm{m}})\)
Bảng biến thiên:
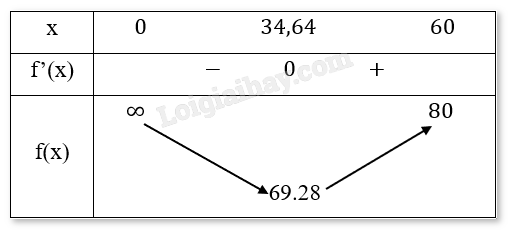
Nhận thấy tại vị trí x=34,64 thì giá trị của f(x) là nhỏ nhất
Tính \(y\): \(y = \frac{{600}}{x} \approx \frac{{600}}{{34,64}} \approx 17,32(\;{\rm{m}})\)
Tính chi phí:
\(L = 2x + 4y = 2.34,64 + 4.17,32 \approx 138,56m\)
\(C = 60000 \times 135,56 \approx 8313600\)
Kết luận: Để chi phí xây dựng hàng rào là thấp nhất thì
- Chiều dài của hình chữ nhật ABCD: \(x \approx 34,64\)m
- Chiều rộng của hình chữ nhật ABCD: \(y \approx 17,32\)m
- Tổng chi phí xây dựng hàng rào: 8313600 đồng.
