Câu hỏi/bài tập:

Người ta cần thiết kế một cái lon có dạng hình trụ có thể tích là 1 lít (Hình 1.41). Tính tỉ lệ chiều cao và bán kính đáy hình trụ này để tổng chi phí làm vỏ lon (bao gồm cả hai đáy) là nhỏ nhất.
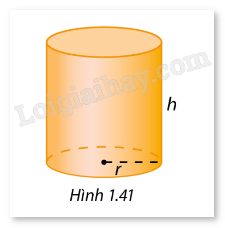

- Đặt bán kính đáy là ? và chiều cao là ℎ của hình trụ.
- Tính diện tích toàn phần của hình trụ dựa trên bán kính và chiều cao.
- Viết hàm chi phí cần tối ưu và điều kiện ràng buộc.
- Khảo sát hàm chi phí để tìm giá trị tối ưu.

Gọi bán kính đáy là ? (? >0) và chiều cao là ℎ (ℎ>0) của hình trụ.
Thể tích hình trụ: \(V = \pi {r^2}h = 1000(c{m^3})\)
Diện tích xung quanh của hình trụ là: \({A_{xq}} = 2\pi rh\)
Advertisements (Quảng cáo)
Diện tích của hai đáy là: \({A_{2đáy}} = 2\pi {r^2}\)
Tổng diện tích bề mặt: \(A = {A_{xq}} + {A_{2d\’a y}} = 2\pi rh + 2\pi {r^2} = 2\pi r.\frac{{1000}}{{\pi {r^2}}} + 2\pi {r^2} = \frac{{2000}}{r} + 2\pi {r^2}\)
Tìm giá trị cực trị: \(f(r) = \frac{{2000}}{r} + 2\pi {r^2}\)
- Tính đạo hàm: \(f'(r) = - \frac{{2000}}{{{r^2}}} + 4\pi r\)
- Cho đạo hàm bằng 0: \( - \frac{{2000}}{{{r^2}}} + 4\pi r = 0 \Rightarrow 4\pi r = \frac{{2000}}{{{r^2}}} \Rightarrow {r^3} = \frac{{2000}}{{4\pi }} = \frac{{500}}{\pi } \Rightarrow r \simeq 5,42(cm)\)
Bảng biến thiên:
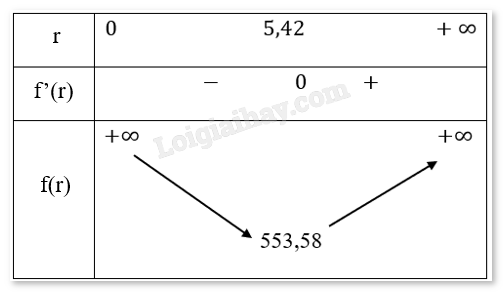
Nhận thấy f(r) đạt giá trị nhỏ nhất tại r ≈ 5,42
Vậy để tổng chi phí làm vỏ lon nhỏ nhất thì:
- Bán kính đáy của hình trụ: r ≈ 5,42 cm
- Chiều cao của hình trụ: \(h = \frac{{1000}}{{\pi {r^2}}} = \frac{{1000}}{{3,14.{{(5,42)}^2}}} \approx 10,84\)cm
- Tỉ lệ chiều cao và bán kính: \(\frac{h}{r} \approx \frac{{10,84}}{{5,42}} \approx 2\)
