
Lập bảng biến thiên, tìm khoảng đơn điệu và cực trị (nếu có) của hàm số:
a) \(y = - {x^3} + 2{x^2} - x - 7\)
b) \(y = \frac{{x - 6}}{{1 - 2x}}\)
c) \(y = \sqrt {4x - {x^2}} \)

- Tìm tập xác định của hàm số
- Tính đạo hàm và giới hạn của hàm số
- Xét sự biến thiên của hàm số

a)
- Tập xác định: D = R.
- Sự biến thiên:
Giới hạn:
\(\mathop {\lim }\limits_{x \to + \infty } f(x) = \mathop {\lim }\limits_{x \to + \infty } \left( { - {x^3} + 2{x^2} - x - 7} \right) = \mathop {\lim }\limits_{x \to + \infty } \left[ { - {x^3}\left( {1 - \frac{2}{x} + \frac{1}{{{x^2}}} + \frac{7}{{{x^3}}}} \right)} \right] = - \infty \)
\(\mathop {\lim }\limits_{x \to - \infty } f(x) = \mathop {\lim }\limits_{x \to - \infty } \left( { - {x^3} + 2{x^2} - x - 7} \right) = \mathop {\lim }\limits_{x \to - \infty } \left[ { - {x^3}\left( {1 - \frac{2}{x} + \frac{1}{{{x^2}}} + \frac{7}{{{x^3}}}} \right)} \right] = + \infty \)
Ta có: \({y^\prime } = - 3{x^2} + 4x - 1\)
\({y^\prime } = 0 \leftrightarrow - 3{x^2} + 4x - 1 = 0 \leftrightarrow x = 1{\rm{ }}\)hoặc \(x = \frac{1}{3}\)
Bảng biến thiên:
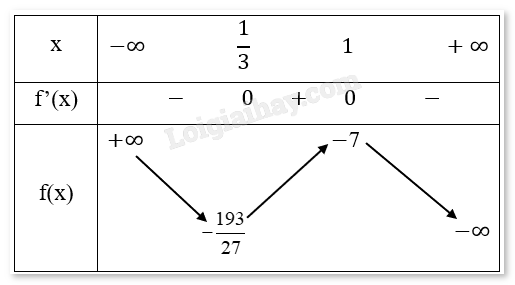
Chiều biến thiên: Hàm số nghịch biến trên các khoảng (−∞,\(\frac{1}{3}\)) và (1,∞), đồng biến trên khoảng (\(\frac{1}{3}\),1).
Cực trị: Hàm số đạt cực tiểu tại \(x = \frac{1}{2},{y_{CT}} = - \frac{{193}}{{27}}\)
Hàm số đạt cực đại tại \(x = 1,{y_{CD}} = - 7\)
b)
Advertisements (Quảng cáo)
- Tập xác định: \({\rm{D}} = {\rm{R}}\backslash \left\{ {\frac{1}{2}} \right\}\).
- Sự biến thiên:
Giới hạn, tiệm cận:
\(\mathop {\lim }\limits_{x \to + \infty } f(x) = \mathop {\lim }\limits_{x \to + \infty } \frac{{x - 6}}{{1 - 2x}} = - \frac{1}{2}\)
\(\mathop {\lim }\limits_{x \to - \infty } f(x) = \mathop {\lim }\limits_{x \to - \infty } \frac{{x - 6}}{{1 - 2x}} = - \frac{1}{2}\)
Suy ra đường thẳng \({\rm{y}} = - \frac{1}{2}\) là đường tiệm cận ngang của đồ thị hàm số đã cho.
\(\mathop {\lim }\limits_{x \to {{\frac{1}{2}}^ + }} f(x) = \mathop {\lim }\limits_{x \to {{\frac{1}{2}}^ + }} \frac{{x - 6}}{{1 - 2x}} = + \infty \)
\(\mathop {\lim }\limits_{x \to {{\frac{1}{2}}^ - }} f(x) = \mathop {\lim }\limits_{x \to {{\frac{1}{2}}^ - }} \frac{{x - 6}}{{1 - 2x}} = - \infty \)
Suy ra đường thẳng \({\rm{x}} = \frac{1}{2}\). là đường tiệm cận đứng của đồ thị hàm số đã cho.
Ta có: \({y^\prime } = \frac{{ - 11}}{{{{(1 - 2x)}^2}}}
Suy ra hàm số nghịch biến trên tập xác định.
Bảng biến thiên:
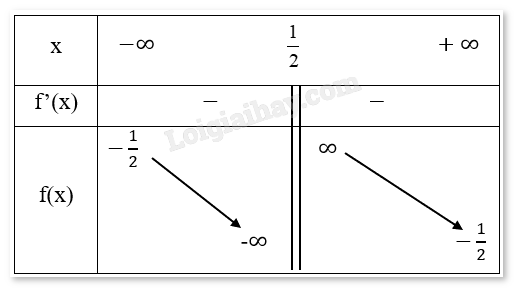
Chiều biến thiên: Hàm số nghịch biến trên \(\left( { - \infty ,\frac{1}{2}} \right)\). và \(\left( {\frac{1}{2}, + \infty } \right)\).
Cực trị: Hàm số không có cực trị.
c)
- Tập xác định: D = [0,4].
- Đạo hàm: \(f'(x) = \frac{{4 - 2x}}{{2\sqrt {4x - {x^2}} }} = \frac{{2 - x}}{{\sqrt {4x - {x^2}} }}\)
- Giải phương trình \(f'(x) = 0\):
\(\begin{array}{l}\frac{{2 - x}}{{\sqrt {4x - {x^2}} }} = 0\\ \Rightarrow 2 - x = 0\\ \Leftrightarrow x = 2\end{array}\)
- Bảng biến thiên:
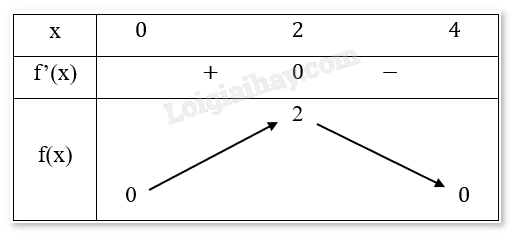
- Chiều biến thiên: Hàm số đồng biến trên khoảng [0,2) và nghịch biến trên khoảng (2,4].
- Hàm số đạt cực đại tại và không có cực tiểu.
