
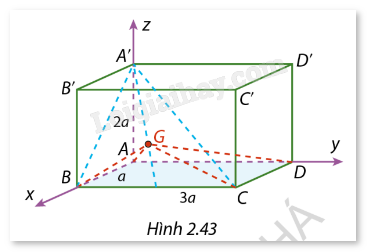
Trong không gian Oxyz, cho hình hộp chữ nhật ABCD.A’B’C’D’ có đỉnh A trùng với gốc tọa độ và các đỉnh B, D, A’ tương ứng thuộc các tia Ox, Oy, Oz như trong Hình 2.43. Cho biết AB = a, AD = 3a, AA’ = 2a \ (a > 0). Gọi G là trọng tâm của tam giác A’BC.
a) Tìm toạ độ điểm G.
b) Tính khoảng cách từ G đến mặt phẳng (ABCD).
c) Tính thể tích khóp G.ABCD.

a) Sử dụng công thức trọng tâm của tam giác trong không gian Oxyz.
b) Sử dụng công thức khoảng cách từ một điểm đến một mặt phẳng trong không gian.
Advertisements (Quảng cáo)
c) Sử dụng công thức thể tích khối chóp trong không gian.

a) Tọa độ các điểm \(B(a;0;0)\), \(C(0;3a;0)\), \(A'(0;0;2a)\). Tọa độ của điểm \(G\) - trọng tâm tam giác A’BC:
\(G\left( {\frac{{0 + a + 0}}{3},\frac{{0 + 0 + 3a}}{3},\frac{{2a + 0 + 0}}{3}} \right) = G\left( {\frac{a}{3};a;\frac{{2a}}{3}} \right)\)
b) Phương trình mặt phẳng \((ABCD)\) là: \(z = 0\). Khoảng cách từ \(G\left( {\frac{a}{3};a;\frac{{2a}}{3}} \right)\) đến mặt phẳng \((ABCD)\) là:
\(d = \left| {\frac{{2a}}{3} - 0} \right| = \frac{{2a}}{3}\)
c) Thể tích khối chóp G.ABCD: Sử dụng công thức thể tích khối chóp với chiều cao là khoảng cách từ \(G\) đến mặt phẳng \((ABCD)\) và diện tích đáy là diện tích hình chữ nhật ABCD:
\(V = \frac{1}{3} \times {S_{ABCD}} \times d = \frac{1}{3} \times (AB \times AD) \times \frac{{2a}}{3} = \frac{1}{3} \times a \times 3a \times \frac{{2a}}{3} = \frac{{2{a^3}}}{3}\)
