
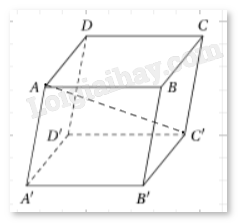
Cho hình hộp ABCD.A’B’C’D’ có tất cả các cạnh đều bằng a và
\(\widehat {BAA’} = \widehat {BAD} = \widehat {DAA’} = {60^\circ }\). Tính độ dài đường chéo AC’.

Sử dụng quy tắc hình hộp và công thức tính tích vô hướng của vectơ, từ đó ta có công thức tính độ dài của \(\overrightarrow {AC’} \) là:
\(|\overrightarrow {AC’} | = \sqrt {|\overrightarrow {AB} {|^2} + |\overrightarrow {AD} {|^2} + |\overrightarrow {AA’} {|^2} + 2\overrightarrow {AB} \cdot \overrightarrow {AD} + 2\overrightarrow {AB} \cdot \overrightarrow {AA’} + 2\overrightarrow {AD} \cdot \overrightarrow {AA’} } \)

Vì tất cả các cạnh đều bằng a và các góc giữa các cặp vectơ đều là \({\rm{\backslash }}({60^\circ }{\rm{ \backslash }})\), ta có:
\(|\overrightarrow {AB} | = |\overrightarrow {AD} | = |\overrightarrow {AA’} | = a\)
Tích vô hướng giữa các cặp vectơ:
Advertisements (Quảng cáo)
\(\overrightarrow {AB} \cdot \overrightarrow {AD} = {a^2}\cos {60^\circ } = \frac{{{a^2}}}{2}\)
\(\overrightarrow {AB} \cdot \overrightarrow {AA’} = {a^2}\cos {60^\circ } = \frac{{{a^2}}}{2}\)
\(\overrightarrow {AD} \cdot \overrightarrow {AA’} = {a^2}\cos {60^\circ } = \frac{{{a^2}}}{2}\)
Vì ABCD.A’B’C’D’ nên:
\(\overrightarrow {AC’} = \overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {AA’} \)
Suy ra:
\(|\overrightarrow {AC’} | = \sqrt {|\overrightarrow {AB} {|^2} + |\overrightarrow {AD} {|^2} + |\overrightarrow {AA’} {|^2} + 2\overrightarrow {AB} \cdot \overrightarrow {AD} + 2\overrightarrow {AB} \cdot \overrightarrow {AA’} + 2\overrightarrow {AD} \cdot \overrightarrow {AA’} } \)
Tính độ dài đường chéo AC’:
\(|\overrightarrow {AC’} | = \sqrt {{a^2} + {a^2} + {a^2} + 2\left( {\frac{{{a^2}}}{2}} \right) + 2\left( {\frac{{{a^2}}}{2}} \right) + 2\left( {\frac{{{a^2}}}{2}} \right)} \)
\(|\overrightarrow {AC’} | = \sqrt {3{a^2} + 3{a^2}} = \sqrt {6{a^2}} = a\sqrt 6 \)
Vậy độ dài đường chéo \(AC’\) là \(a\sqrt 6 \).
