Câu hỏi/bài tập:
Cho hàm số \(y = f(x) = - {x^3} + 3{x^2} - 4.\)
a) Tập xác định của hàm số \(f(x)\) là gì?
b) Hàm số \(f(x)\) đồng biến, nghịch biến trên các khoảng nào?
c) Hàm số \(f(x)\) đạt cực đại và cực tiểu tại những điểm nào?
d) Đồ thị hàm số \(y = f(x)\) có tiệm cận hay không?

a) Tập xác định: Đối với một hàm đa thức, tập xác định là toàn bộ các số thực \(R\).
b) Xét tính đơn điệu:
- Tính \({f^\prime }(x)\).
- Tìm các điểm mà tại đó \({f^\prime }(x)\) bằng 0.
- Lập bảng biến thiên.
c) Tìm cực trị: Từ bảng biến thiên, suy ra các điểm cực trị
d) Tiệm cận: Đối với hàm đa thức, không tồn tại tiệm cận ngang, đứng hay xiên.

a) Hàm số \(f(x) = - {x^3} + 3{x^2} - 4\) là một đa thức bậc ba, nên D=R.
b) Xét tính đơn điệu
Tính \({f^\prime }(x):{f^\prime }(x) = - 3{x^2} + 6x\)
Advertisements (Quảng cáo)
Tìm nghiệm khi \({f^\prime }(x) = 0\)
\({f^\prime }(x) = 0 \leftrightarrow - 3{x^2} + 6x = 0\)
\( \leftrightarrow - 3x(x - 2) = 0\)
\( \leftrightarrow x = 0\)hoặc \(x = 2\)
Tính giới hạn
\(\begin{array}{l}\mathop {\lim }\limits_{x \to + \infty } f(x) = \mathop {\lim }\limits_{x \to + \infty } \left( { - {x^3} + 3{x^2} - 4} \right) = \mathop {\lim }\limits_{x \to + \infty } \left[ { - {x^3}\left( {1 + \frac{3}{x} - \frac{4}{{{x^3}}}} \right)} \right] = - \infty \\\end{array}\)
\(\mathop {\lim }\limits_{x \to - \infty } f(x) = \mathop {\lim }\limits_{x \to - \infty } \left( { - {x^3} + 3{x^2} - 4} \right) = \mathop {\lim }\limits_{x \to - \infty } \left[ { - {x^3}\left( {1 + \frac{3}{x} - \frac{4}{{{x^3}}}} \right)} \right] = + \infty \)
Bảng biến thiên:
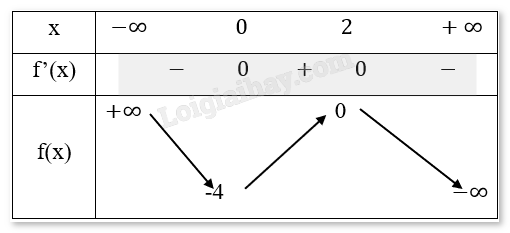
Kết luận:
- Hàm số nghịch biến trên các khoảng \(( - \infty ;0)\) và \((2; + \infty )\).
- Hàm số đồng biến trên khoảng \((0;2)\).
c) Tìm cực trị
Dựa vào bảng biến thiên, ta có thể kết luận:
- Hàm số đạt cực tiểu tại \(x = 0\)
- Hàm số đạt cực đại tại \(x = 2\)
d) Hàm số \(f(x)\) là một đa thức bậc ba, vì vậy nó không có tiệm cận ngang, đứng hay xiên. Đồ thị của hàm số không có tiệm cận.
