Câu hỏi/bài tập:
Cho hàm số \(y = \frac{x^2{{} + 4}}{x}\)
a) Xét tính liên tục của hàm số đã cho trên mỗi đoạn\([ - 5; - 1]\) và \([ - 4;3]\)
b) Tính giá trị lớn nhất, giá trị nhỏ nhất (nếu có) của hàm số đã cho trên các đoạn\([ - 5; - 1]\) và \([ - 4;3]\)

a) Tìm tập xác định của hàm số
b) Bước 1: Tính \(y’\)
Bước 2: Lập bảng biến thiên
Bước 3: Xác định giá trị lớn nhất, giá trị bé nhất của hàm số trên các đoạn

a) TXĐ: \(x \in R/\{ 0\} \)
Advertisements (Quảng cáo)
Vậy hàm số liên tục trên đoạn \([ - 5; - 1]\)
Và không liên tục trên đoạn \([ - 4;3]\)
Ta có \(y’ = \frac{{{x^2} - 4}}{{{x^2}}}\)
Xét \(y’ = 0\) \( \Rightarrow {x^2} - 4 = 0\)\( \Rightarrow \left[ \begin{array}{l}x = 2\\x = - 2\end{array} \right.\)
Từ đó ta có bảng biến thiên là
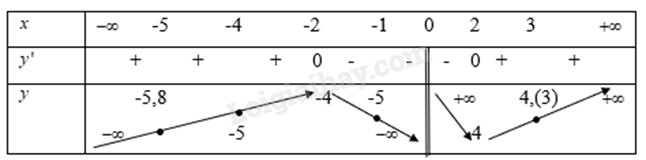
b) Từ bảng biến thiên ta có
Hàm số\ (y = \frac{{{x^2} + 4}}{x}\) đạt giá trị lớn nhất trên khoảng\([ - 5; - 1]\) tại \(x = 1\) khi đó
Hàm số \(y = \frac{{{x^2} + 4}}{x}\) đạt giá trị bé nhất trên khoảng\([ - 5; - 1]\) tại điểm \(x = - 5\) khi đó
Hàm số \(y = \frac{{{x^2} + 4}}{x}\) đạt giá trị lớn nhất \([ - 4;3]\) trên khoảng tại điểm
Hàm số \(y = \frac{{{x^2} + 4}}{x}\) đạt giá trị bé nhất \([ - 4;3]\) trên khoảng tại điểm
