Câu hỏi/bài tập:
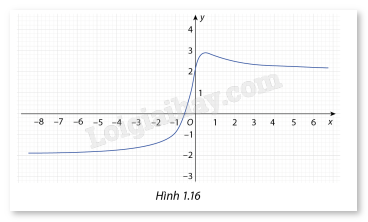
Cho hàm số \(y = f(x) = \frac{{4x + 2}}{{\sqrt {4{x^2} + 1} }}\) có đồ thị như Hình 1.16
a) Tìm các đường tiệm cận ngang của đô thị nếu có.
b) Vẽ các đường tiệm cận ngang vừa tìm được nếu có.

a) Xét \(\mathop {\lim }\limits_{x \to + \infty } f(x)\) và \(\mathop {\lim }\limits_{x \to - \infty } f(x)\)
Advertisements (Quảng cáo)
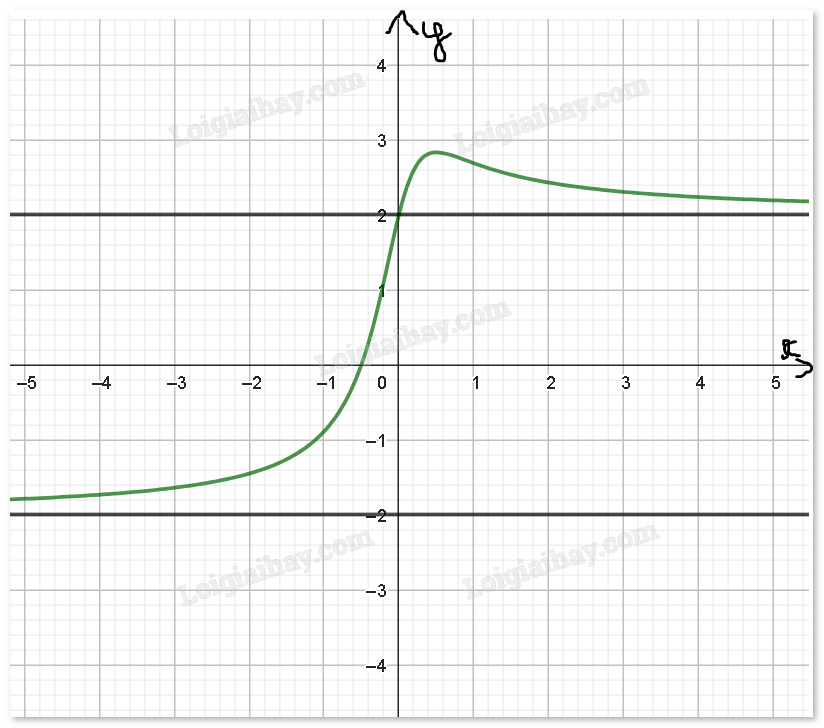
b) Trên trục Oy tại điểm có giá trị bằng 2 vẽ một đường thẳng song song với Ox. Trên trục Oy tại điểm có giá trị bằng -2 vẽ một đường thẳng song song với Ox.

a) Ta có:
\(\mathop {\lim }\limits_{x \to + \infty } \frac{{4x + 2}}{{\sqrt {4{x^2} + 1} }}\;\)=\(\mathop {\lim }\limits_{x \to + \infty } \left[ {2\left( {\frac{{2x + 1}}{{\sqrt {4{x^2} + 1} }}} \right)} \right]\;\) =\(\mathop {\lim }\limits_{x \to + \infty } \left[ {2\left( {\sqrt {\frac{{4{x^2} + 4x + 1}}{{4{x^2} + 1}}} } \right)\;} \right]\;\)= \(\mathop {\lim }\limits_{x \to + \infty } \left[ {2\left( {\sqrt {1 + \frac{{4x}}{{4{x^2} + 1}}} } \right)\;} \right]\;\;\)=\(\mathop {\lim }\limits_{x \to + \infty } \left[ {2\left( {\sqrt {1 + \frac{{\frac{4}{x}}}{{4 + \frac{1}{x}}}} } \right)\;} \right]\;\;\;\) = 2.
\(\mathop {\lim }\limits_{x \to - \infty } \frac{{4x + 2}}{{\sqrt {4{x^2} + 1} }}\;\)=\(\mathop {\lim }\limits_{x \to - \infty } \left[ {2\left( {\frac{{2x + 1}}{{\sqrt {4{x^2} + 1} }}} \right)} \right]\;\) =\(\mathop {\lim }\limits_{x \to - \infty } \left[ {2\left( {\sqrt {\frac{{4{x^2} + 4x + 1}}{{4{x^2} + 1}}} } \right)\;} \right]\;\)= \(\mathop {\lim }\limits_{x \to + \infty } \left[ {2\left( {\sqrt {1 + \frac{{4x}}{{4{x^2} + 1}}} } \right)\;} \right]\;\;\)=\(\mathop {\lim }\limits_{x \to - \infty } \left[ {2\left( {\sqrt {1 + \frac{{\frac{4}{x}}}{{4 + \frac{1}{x}}}} } \right)\;} \right]\;\;\;\) = - 2.
b)