Câu hỏi/bài tập:
Cho hàm số \(y = \frac{{x + 1}}{{x - 2}}\)có đồ thị (C ) như Hình 1.17.
a) Nêu nhận xét về khoảng cách từ điểm \(M(x;y) \in (C)\)đến đường thảng x=2 khi \(x \to 2\)
b) Tính các giới hạn \(\mathop {\lim }\limits_{x \to {2^ + }} f(x)\) và \(\mathop {\lim }\limits_{x \to {2^ - }} f(x)\)
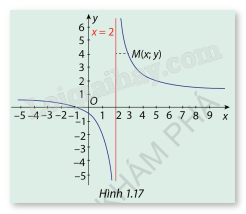

a) Nhìn đồ thị hàm số rồi nhận xét
Advertisements (Quảng cáo)
b) Phân tích, rồi tính \(\mathop {\lim }\limits_{x \to {2^ + }} f(x)\) và \(\mathop {\lim }\limits_{x \to {2^ - }} f(x)\)

a) Dựa vào đồ thị hàm số ta thấy:
Khi và thì khoảng cách giữa đồ thị (C) với đường thẳng x = 2 càng nhỏ
b) Ta có \(f\left( x \right)\; = \frac{{x + 1}}{{x - 2}} = 1 + \frac{3}{{x - 2}} = + \infty \;\;\)
\(f\left( x \right)\; = \frac{{x + 1}}{{x - 2}} = 1 + \frac{3}{{x - 2}} = - \infty \;\;\)
