Bước 1: Tính\(f'(x)\). Phân tích, đưa ra lời giải Câu hỏi Luyện tập 1 trang 11 SGK Toán 12 Cùng khám phá - Bài 2. Giá trị lớn nhất - giá trị nhỏ nhất của hàm số.
Câu hỏi/bài tập:
Tìm giá trị lớn nhất, giá trị bé nhất của hàm số\(y = f(x) = {x^3} - 6{x^2} + 9x + 1\) trên nửa khoảng\([ - 1;4)\)

Bước 1: Tính\(f'(x)\)
Bước 2: Lập bảng biến thiên
Bước 3: Xác định giá trị lớn nhất, giá trị bé nhất của hàm số trên nửa khoảng \([ - 1;4)\)

Ta có: \(f'(x) = 3{x^2} - 12x + 9\)
Advertisements (Quảng cáo)
Xét \(f'(x) = 0\)
\( \Rightarrow 3{x^2} - 12x + 9 = 0\)
\( \Rightarrow \left[ \begin{array}{l}x = 3\\x = 1\end{array} \right.\)
Ta có bảng biến thiên là
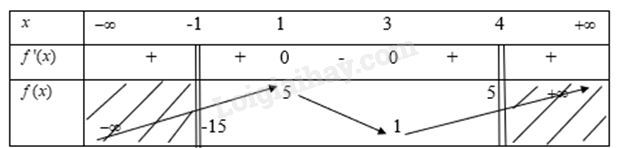
Từ bảng biến thiên ta thấy
Hàm số đạt giá trị cực đại trong nửa khoảng \([ - 1;4)\) tại \(x = 1\) khi đó \(y = 5\)
Và đạt giá trị cực tiểu trong nửa khoảng \([ - 1;4)\) tại\(x = - 1\) khi đó \(y = - 15\)
