Nhìn đồ thị hàm số rồi rút ra điểm có tọa dộ thấp nhất. Lời giải bài tập, câu hỏi Câu hỏi Hoạt động 1 trang 10 SGK Toán 12 Cùng khám phá - Bài 2. Giá trị lớn nhất - giá trị nhỏ nhất của hàm số.
Câu hỏi/bài tập:
Cho hàm số \(y = f(x) = {x^2} - 4x + 3\) có đồ thị như hình 1.7
a) Tìm tọa độ điểm thấp nhất của đồ thị hàm số \(f(x)\) đã cho
b) Khi \(x\)thay đổi trên đoạn \([1;4]\), tìm \({x_0} \in [1;4]\) để \(f({x_0})\)có giá trị lớn nhất
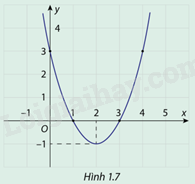

a) Nhìn đồ thị hàm số rồi rút ra điểm có tọa dộ thấp nhất
b) Lập bảng biến thiên rồi tìm \({x_0} \in [1;4]\) để \(f({x_0})\) lớn nhất
Advertisements (Quảng cáo)

a) Dựa vào dồ thị hàm số ta thấy tọa độ điểm thấp nhất là (2;-1)
b) Ta có: \(y’ = 2x - 4\)
Xét \(y’ = 0\)\( \Rightarrow 2x - 4 = 0\) \( \Rightarrow x = 2\)
Ta có bảng biến thiên
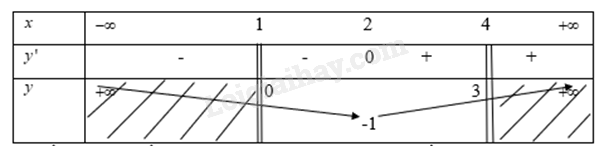
Từ bảng biến thiên ta thấy tại \({x_0} = 4\) thì \(f({x_0})\) đạt giá trị lớn nhất
