Câu hỏi/bài tập:
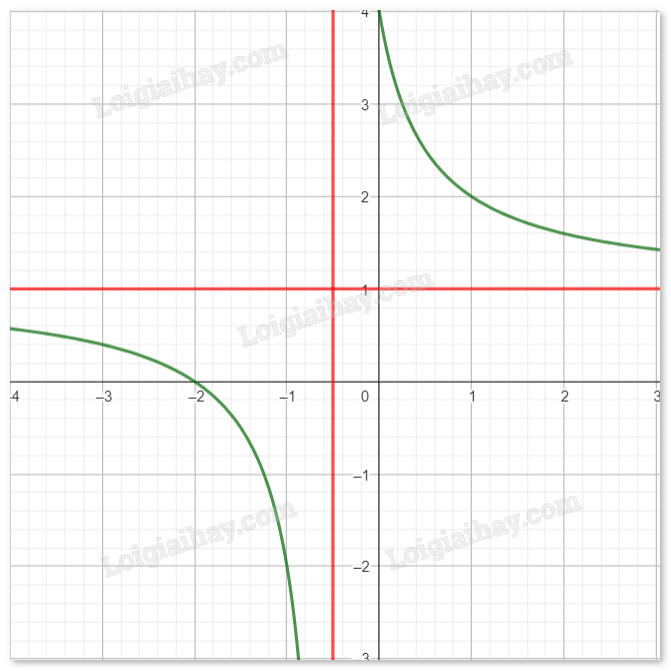
Khảo sát sự biến thiên và vẽ đồ thị của hàm số \(y = f(x) = \frac{{2x + 4}}{{2x + 1}}.\)

- Tìm tập xác định của hàm số.
- Xét sự biến thiên của hàm số.
- Vẽ đồ thị hàm số.

- Tập xác định: \({\rm{D}} = {\rm{R}}\backslash \left\{ {\frac{{ - 1}}{2}} \right\}\).
- Sự biến thiên:
Giới hạn, tiệm cận:
\(\mathop {\lim }\limits_{x \to + \infty } f(x) = \mathop {\lim }\limits_{x \to + \infty } \frac{{2x + 4}}{{2x + 1}} = 1.\)
\(\mathop {\lim }\limits_{x \to - \infty } f(x) = \mathop {\lim }\limits_{x \to - \infty } \frac{{2x + 4}}{{2x + 1}} = 1.\)
Advertisements (Quảng cáo)
Suy ra đường thẳng \({\rm{y}} = 1\) là đường tiệm cận ngang của đồ thị hàm số đã cho
\(\mathop {\lim }\limits_{x \to {{\frac{{ - 1}}{2}}^ + }} f(x) = \mathop {\lim }\limits_{x \to {{\frac{{ - 1}}{2}}^ + }} \frac{{2x + 4}}{{2x + 1}} = + \infty \)
\(\mathop {\lim }\limits_{x \to {{\frac{{ - 1}}{2}}^ - }} f(x) = \mathop {\lim }\limits_{x \to {{\frac{{ - 1}}{2}}^ - }} \frac{{2x + 4}}{{2x + 1}} = - \infty \)
Suy ra đường thẳng \({\rm{x}} = \frac{{ - 1}}{2}\). là đường tiệm cận đứng của đồ thị hàm số đã cho
Ta có: \({y^\prime } = \frac{{ - 6}}{{{{(2x + 1)}^2}}} < 0.\)
Suy ra hàm số nghịch biến trên tập xác định.
Bảng biến thiên:
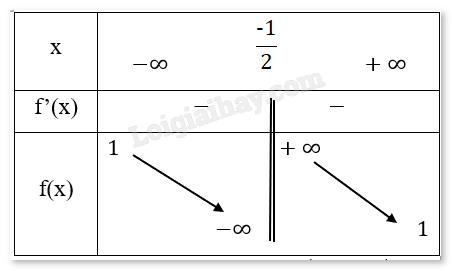
Chiều biến thiên: Hàm số nghịch biến trên \(\left( { - \infty ,\frac{{ - 1}}{2}} \right)\) và \(\left( {\frac{{ - 1}}{2}, + \infty } \right)\)
Cực trị: Hàm số không có cực trị.
- Vẽ đồ thị: