Câu hỏi/bài tập:
Một chi tiết máy có dạng khối nón với bán kính đáy là 6 cm và chiều cao là 8 cm. Người ta cần khoan từ đáy khối nón lên phía trên một khối trụ có bán kính đáy là r (r > 0)và có tâm của đáy trùng tâm của đáy khối nón như Hình 1.32. Xác định r sao cho phần thể tích khối trụ có được là lớn nhất.
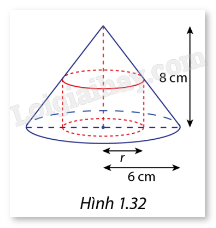

- Biểu diễn thể tích khối trụ cần khoan trong khối nón
- Biểu diễn chiều cao h của khối trụ theo bán kính r
- Xác giá trị r để thể tích khối trụ V lớn nhất bằng cách tìm giá trị lớn nhất của V trong khoảng (0, \( + \infty )\).

Ta có thể tích khối trụ là:
\(V = \pi {r^2}h\)
Sử dụng tỷ lệ hình học trong tam giác đồng dạng:
Advertisements (Quảng cáo)
\(\frac{h}{8} = \frac{{6 - r}}{6} \to h = 8.\frac{{6 - r}}{6} = 8 - \frac{{8r}}{6} = 8 - \frac{{4r}}{3}\)
Thay h vào công thức tính thể tích V:
\(V = \pi {r^2}\left( {8 - \frac{{4r}}{3}} \right) = \pi {r^2} \cdot \frac{{24 - 4r}}{3} = \pi \cdot \frac{{24{r^2} - 4{r^3}}}{3} = \frac{\pi }{3}\left( {24{r^2} - 4{r^3}} \right)\)
Đạo hàm V theo r:
\(\frac{{dV}}{{dr}} = \frac{\pi }{3}\left( {48r - 12{r^2}} \right) = \frac{\pi }{3} \cdot 12r(4 - r) = 4\pi r(4 - r)\)
Với \(\frac{{dV}}{{dr}} = 0\) thì ta có 2 nghiệm r là \(r = 0\) hoặc \(r = 4\) (Loại \(r = 0\) vì \(r > 0\))
Lập bảng biến thiên của hàm số \(f(x) = \frac{\pi }{3}\left( {24{x^2} - 4{x^3}} \right)\)
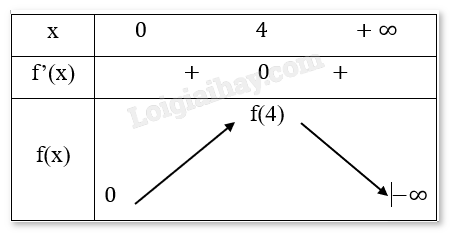
Nhận thấy khi x = 0 thì giá trị của f(x) là lớn nhất
Vậy giá trị bán kính r sao cho phần thể tích khối trụ có được là lớn nhất là r = 4cm.
