Câu hỏi/bài tập:
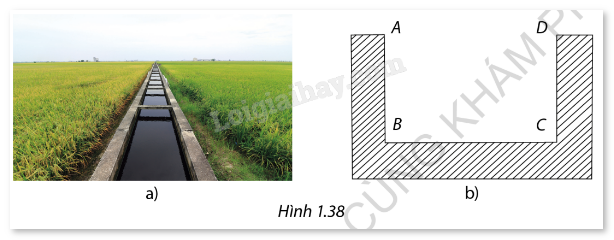
Hình 1.38a là một mương dẫn nước thủy lợi tại một địa phương. Phần không gian trong mương để nước chảy có mặt cắt ngang là một hình chữ nhật ABCD (Hình 1.36b). Với điều kiện lưu lượng nước qua mương cho phép ở đây thì diện tích mặt cắt ABCD là 1,2m2. Để đảm bảo yêu cầu kỹ thuật tốt nhất cho mương, người ta cần thiết kế sao cho tổng độ dài AB+BC+CD là ngắn nhất.
a) Đặt BC= x, tính y=AB+BC+CD theo x.
b) Khảo sát hàm số y=f(x) tìm được ở câu a, từ đó tính x để y nhỏ nhất, biết rằng theo quy định thì đoạn BC (chiều rộng đáy mương) phải dưới 10 m.

a) Sử dụng công thức diện tích để thiết lập phương trình liên hệ giữa các biến.
Biểu diễn tổng chiều dài cần tối thiểu hóa theo biến ?.
b) Khảo sát sự biến thiên của hàm số.
Tìm giá trị ? để hàm số đạt giá trị nhỏ nhất trong khoảng xác định.

a) Gọi \({\rm{AB}} = {\rm{CD}} = {\rm{h}}\). Ta có diện tích hình chữ nhật ABCD là:
\(S = BC \cdot AB = x.h = 1,2\;{{\rm{m}}^2}\).
Từ đó suy ra \(h = \frac{{1,2}}{x}\).
Tổng chiều dài cần tối thiểu hóa là: \(y = AB + BC + CD = h + x + h = 2h + x\).
Advertisements (Quảng cáo)
Thay \(h = \frac{{1,2}}{x}\) vào, ta được: \(y = 2 \cdot \frac{{1,2}}{x} + x = \frac{{2,4}}{x} + x\).
b) Khảo sát hàm số \(y = f(x) = \frac{{2,4}}{x} + x\).
- Tập xác định: \(D = \{ x > 0,x \in R\} \).
- Sự biến thiên:
Giới hạn:
\(\mathop {\lim }\limits_{x \to 0 + } y = \mathop {\lim }\limits_{x \to {0^ + }} \left( {\frac{{2,4}}{x} + x} \right) = \mathop {\lim }\limits_{x \to {0^ + }} \left( {\frac{{2,4}}{x} + x} \right) = \infty \).
\(\mathop {\lim }\limits_{x \to {0^ - }} y = \mathop {\lim }\limits_{x \to {0^ - }} \left( {\frac{{2,4}}{x} + x} \right) = \mathop {\lim }\limits_{x \to {0^ - }} \left( {\frac{{2,4}}{x} + x} \right) = - \infty \).
Suy ra \({\rm{x}} = 0\) là tiệm cận đứng của hàm số.
Khi \(x \to \pm \infty ,\frac{{2,4}}{x} \to 0\) nên \(y = x\) là tiệm cận xiên của hàm số.
Ta có: \({y^\prime } = - \frac{{2,4}}{{{x^2}}} + 1\).
\({y^\prime } = 0 \Rightarrow - \frac{{2,4}}{{{x^2}}} + 1 = 0 \Rightarrow \frac{{2,4}}{{{x^2}}} = 1 \Rightarrow x = 2,4\) vì \(x > 0.\)
Bảng biến thiên:
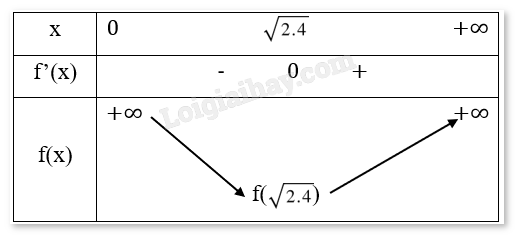
Cực trị: Hàm số đạt cực tiểu tại \(x = \sqrt {2,4} \).
Vậy để tổng chiều dài AB+BC+CD là ngắn nhất, ta chọn: \(x = \sqrt {2,4} \approx 1,55\;{\rm{m}}.\)
