1. Tính đơn điệu của hàm số và dấu của đạo hàm
Định lý
|
Cho hàm số y = f(x) có đạo hàm trên khoảng (a;b), (có thể a là \( - \infty \);b là \( + \infty \))
|
Ví dụ: Hàm số \(y = {x^2} - 4x + 2\) có y’ = 2x – 4
- y’ > 0 với \(x \in (2; + \infty )\) nên HS đồng biến trên khoảng \(\left( {2; + \infty } \right)\)
- y’
Định lý mở rộng
|
Cho hàm số y = f(x) có đạo hàm trên khoảng (a;b).
|
2. Cực trị của hàm số
Khái niệm cực trị của hàm số
|
Cho hàm số y = f(x) xác định và liên tục trên khoảng (a;b) (a có thể là \( - \infty \), b có thể là \( + \infty \) ) và điểm \({x_0} \in \left( {a;b} \right)\).
|
Ví dụ: Cho đồ thị của hàm số y = f(x) như sau:
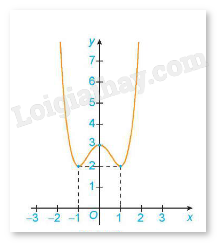
Hàm số đạt cực tiểu tại x = -1 và \({y_{CT}}\)= y(-1) = 2
Hàm số đạt cực đại tại x = 0 và = y(0) = 3
Advertisements (Quảng cáo)
Hàm số đạt cực tiểu tại x = 1 và \({y_{CT}}\)= y(1) = 2
Định lý (điều kiện đủ để hàm số có cực trị)
|
Giả sử hàm số y = f(x) liên tục trên khoảng (a;b) chứa điểm \({x_0}\) và có đạo hàm trên các khoảng \(\left( {a;{x_0}} \right)\) và \(\left( {{x_0};b} \right)\). Khi đó:
|
Ví dụ: Tìm cực trị của hàm số \(y = {x^3} - 6{x^2} + 9x + 30.\)
Tập xác định của hàm số là R.
Ta có: \(y’ = 3{x^2} - 12x + 9\); y’ = 0 \( \Leftrightarrow \)x = 1 hoặc x = 3.
BBT:
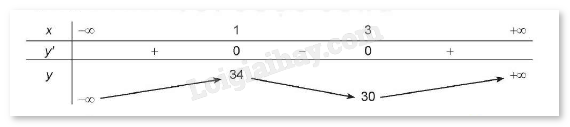
Hàm số đạt cực đại tại x = 1 và = y(1) = 34.
Hàm số đạt cực tiểu tại x = 3 và \({y_{CT}}\)= y(3) = 30.
|
Tổng quát, ta có quy tắc tìm cực trị của hàm số y = f(x) |