Hoạt động (HĐ) 1
Hình 1.2 là đồ thị (C) của hàm số \(y = f(x) = \frac{{ - 1}}{2}{x^2} + 3\)
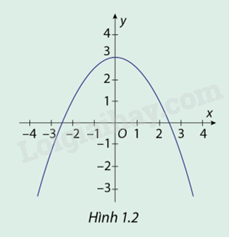
a) Quan sát đồ thị hàm số (C) và chỉ ra các khoảng đồng biến, nghịch biến của hàm số đã cho.
b) Xác định dấu của đạo hàm \(f'(x)\) khi \(x\)thuộc các khoảng đồng biến, nghịch biến ở câu.
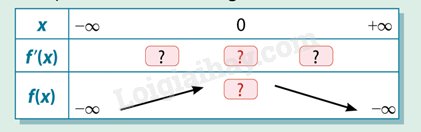
c) Ghi lại và hoàn thành bảng biến thiên sau

a) Sử dụng khái niệm hàm số đồng biến, hàm số nghịch biến trên khoảng (a;b)
Hàm số \(y = f(x)\)gọi là đồng biến trên khoảng \((a;b)\) nếu với mọi \({x_1},{x_2} \in (a;b)\) mà \({x_1}
Hàm số \(y = f(x)\) gọi là nghịch biến trên khoảng \((a;b)\) nếu với mọi \({x_1},{x_2} \in (a;b)\) mà \({x_1} > {x_2}\) thì ta có \(f({x_1})
b) Chọn vài giá trị của x nằm trong khoảng đồng biến , nghịch biến ở câu a rồi thay vào \(f'(x)\)xem \(f'(x)\) có giá trị âm hay dương.
c) Áp dụng kết quả câu a và câu b rồi điền vào

a) Hàm số \(y = f(x)\) xác định trên R
Nhìn hình 1.2 ta thấy:
Hàm số \(f(x) = \frac{{ - 1}}{2}{x^2} + 3\) đồng biến trên khoảng \(( - \infty ;0)\)
Hàm số \(f(x) = \frac{{ - 1}}{2}{x^2} + 3\) nghịch biến trên khoảng \((0; + \infty )\)
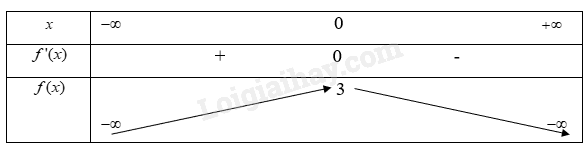
b) Ta có \(f'(x) = - x\)
Ta thấy: Với \(x > 0\)thì \(f'(x)
Với \(x 0\)
c)
Luyện tập (LT) 1
Lập bảng biến thiên và kết luận các khoảng đồng biến, nghịch biến của hàm số.
a) \(y = f(x) = \frac{{2x - 1}}{{x + 3}}\)
b) \(y = f(x) = \cos x\) trên khoảng \((0;2\pi )\)

Bước 1: Xét \(f'(x) = 0\)qua đó tìm x
Bước 2: Xét dấu \(f'(x)\)
Bước 3: lập bảng biến thiên

a) \(y = f(x) = \frac{{2x - 1}}{{x + 3}}\)
Hàm số trên xác định trên R\ {-3}
Ta có: \(f'(x) = \frac{{2(x + 3) - (2x - 1)}}{{{{(x + 3)}^2}}}\)
\(f'(x) = \frac{7}{{{{(x + 3)}^2}}}\)
Vì \(f'(x) > 0\)với \(\forall x \ne - 3\) từ đó ta có bảng biến thiên
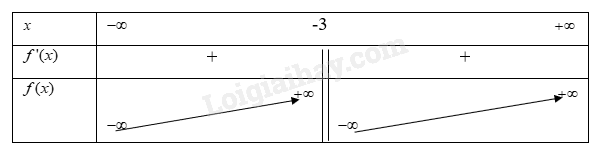
Từ bảng biến thiên ta có,
Hàm số \(y = f(x) = \frac{{2x - 1}}{{x + 3}}\) đồng biến trên khoảng \(( - \infty ; - 3)\)và \(( - 3; + \infty )\)
b) \(y = f(x) = \cos x\) trên khoảng \((0;2\pi )\)
Advertisements (Quảng cáo)
Hàm số trên xác định trên R
Ta có \(y = f'(x) = - \sin x\)
Xét \(f'(x) = - \sin x = 0\) \( \Rightarrow x = k\pi \)
Mà \(x \in (0;2\pi )\) \( \Rightarrow x = \pi \)
Khi đó ta có bảng biến thiên
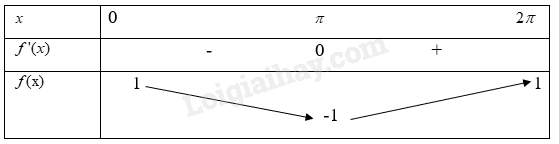
Từ bảng biến thiên ta có
Hàm số \(f(x) = \cos x\) đồng biến trên khoảng\((\pi ;2\pi )\)
Hàm số \(f(x) = \cos x\) nghịch biến trên khoảng\((0;\pi )\)
Hoạt động (HĐ) 2
Cho hàm số \(y = f(x) = {x^3} + 1\)
a) Bằng định nghĩa, hãy cho biết hàm \(f(x)\)có đồng biến trên \(R\) hay không
b) Hãy nhận xét về dấu của đạo hàm \(f'(x)\) trên \(R\)

a) Gọi \({x_1}\), \({x_2}\) sao cho \({x_1},{x_2} \in R\) và\({x_1} > {x_2}\)
Xét dấu của \(f({x_1}) - f({x_2})\)
b) Tính \(f'(x)\) qua đó xét dấu của \(f'(x)\)

a) Gọi \({x_1}\), \({x_2}\) sao cho \({x_1},{x_2} \in R\)và \({x_1} > {x_2}\)
Ta có: \(f({x_1}) - f({x_2})\)= \(({x_1} + 1) - ({x_2} + 1)\)= \({x_1} - {x_2}\)
Mà \({x_1} > {x_2}\) \( \Rightarrow {x_1} - {x_2} > 0\)
Nên \(f({x_1}) - f({x_2}) > 0\) \( \Rightarrow f({x_1}) > f({x_2})\)
Suy ra hàm số \(y = f(x) = {x^3} + 1\) đồng biến trên \(R\)
b) Ta có: \(f'(x) = 3{x^2}\)
Vì \(3{x^2} > 0\) với \(\forall x \in R\)
Nên \(f'(x) > 0\) với \(\forall x \in R\)
Luyện tập (LT) 2
Xét tính đơn điệu của hàm số \(y = \sin x - x\)trên khoảng \(( - \pi ;\pi )\)

Bước 1: tính đạo hàm \(y’\)
Bước 2: xét dấu \(y’\) rồi lập bảng biến thiên
Bước 3: Từ bảng biến thiên nhận xét tính đơn điệu của hàm số

Hàm số đã cho xác định trên
Ta có: \(y’ = \cos x - 1\)
Vì \(\cos x \le 1\)với \(\forall x \in R\)
Nên \(y’ \le 0\)với \(\forall x \in R\)và \(y’ = 0\)tại \(x = 0\)
Khi đó ta có bảng biến thiên:
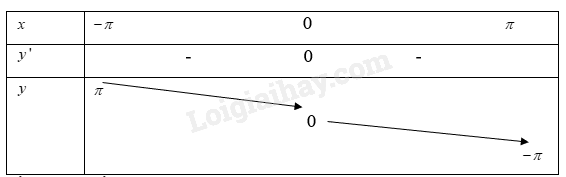
Vậy hàm số nghịch biến trên khoảng \(( - \pi ;\pi )\)
