Hoạt động (HĐ) 3
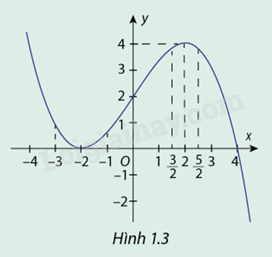
Hàm số \(y = f(x) = - \frac{1}{8}{x^3} + \frac{3}{2}x + 2\) có đồ thị cho ở hình 1.3
a) Giải phương trình \(f'(x) = 0\)
b) Dựa vào đồ thị, só sánh \(f( - 2)\) với các giá trị khi \(x \in ( - 3; - 1)\)
c) Dựa vào đồ thị, só sánh \(f(2)\) với các giá trị khi \(x \in \left( {\frac{3}{2};\frac{5}{2}} \right)\)
a) Tính \(f'(x)\) rồi giải phương trình \(f'(x) = 0\)
b) Dựa vào đồ thị hàm số rồi giải
a) Ta có: \(f'(x) = - \frac{3}{8}{x^2} + \frac{3}{2}\)
Xét \(f'(x) = - \frac{3}{8}{x^2} + \frac{3}{2} = 0\)
\( \Rightarrow {x^2} = 4\)
\( \Rightarrow \left[ \begin{array}{l}x = 2\\x = - 2\end{array} \right.\)
b) Dựa vào đồ thị, giá trị của \(f( - 2)\) luôn bé hơn các giá trị \(f(x)\) khi \(x \in ( - 3; - 1)\)
c) Dựa vào đồ thị, giá trị của \(f(2)\)luôn lớn hơn các giá trị\(f(x)\) khi \(x \in \left( {\frac{3}{2};\frac{5}{2}} \right)\)
Luyện tập (LT) 3
Chỉ ra một điểm cực đại, một điểm cực tiểu của đồ thị hàm số được cho ở hoạt động 3
Áp dụng định nghĩa về cực trị:
Cho hàm số \(y = f(x)\)liên tục trên khoảng \((a;b)\) và điểm \({x_0} \in (a;b)\)
Nếu tồn tại \(h > 0\)sao cho \(f(x)
Nếu tồn tại \(h > 0\)sao cho \(f(x) > f({x_0})\) với mọi \(x \in ({x_0} - h;{x_0} + h) \subset (a;b)\)và \(x \ne 0\)thì ta nói hàm số đạt tiểu đại tại \({x_0}\)
Theo định nghĩa, ta có thể chọn\(h = 1\) ta có, \({x_0} - h = - 3\)và \({x_0} + h = - 1\)
Dựa vào đồ thị hàm số, ta có
\(f(x) > f( - 2)\), với\(\forall x \in ( - 3; - 1)\backslash \{ - 2\} \)
Suy ra \({x_0} = - 2\) là điểm cực tiểu của đồ thị hàm số
Theo định nghĩa, ta có thể chọn \(h = \frac{1}{2}\) ta có, \({x_0} - h = \frac{3}{2}\) và\({x_0} + h = \frac{5}{2}\)
Dựa vào đồ thị hàm số, ta có
\(f(x)
Suy ra \({x_0} = 2\) là điểm đại của đồ thị hàm số
Hoạt động (HĐ) 4
Xét hàm số ở hoạt động 3. Xác định dấu của đạo hàm ở các ô 
tương ứng với thuộc các khoảng trong bảng 1.2. Nêu mỗi liên hệ giữa sự tồn tại cực trị và dấu của đạo hàm.
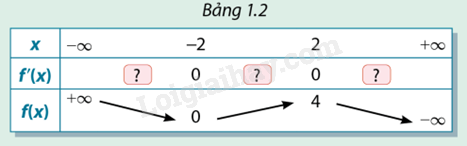
Dựa vào đồ thị hàm số, nếu đồ thị hàm số\(f(x)\) đi xuống thì \(f'(x)\)mang dấu (-)và ngược lại, nếu đồ thị hàm số\(f(x)\) đi lên thì \(f'(x)\) mang dấu (+).
Nhìn vào điểm cực trị trên bảng biến thiên rồi nhận xét.
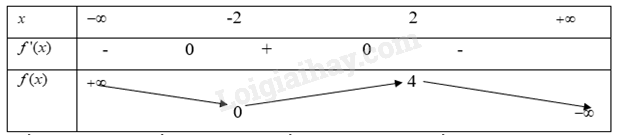
Mối liên hệ giữa sự tồn tại cực trị và dấu của đạo hàm là: Nếu đạo hàm có cực trị thì dấu của đạo hàm bên trái và bên phải điểm cực trị sẽ khác nhau.
Luyện tập (LT) 4
Advertisements (Quảng cáo)
Cho hàm số \(y = f(x)\) liên tục trên đoạn \(\left[ { - 3;3} \right]\)và có đồ thị hàm số như hình 1.4. Hãy xác định các điểm cực trị của hàm số trên khoảng\(\left( { - 3;3} \right)\)
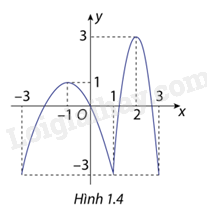
Dựa vào đồ thị hàm số.
Dựa vào đồ thị hàm số, hàm số có 3 điểm cực trị là-1;1;2
Với điểm có cực trị là -1 thì giá trị cực trị là 1
Với điểm có cực trị là 1 thì giá trị cực trị là -3
Với điểm có cực trị là 2 thì giá trị cực trị là 3
Luyện tập (LT) 5
Tìm cực trị của hàm số \(y = f(x) = \frac{{3x + 1}}{{x - 2}}\)
Bước 1: Tính \(f'(x)\)
Bước 2: Lập bảng biến thiên
Bước 3: Xác định cực trị của hàm số
Hàm số trên xác định trên \(R/\{ 2\} \)
Ta có: \(f'(x) = \frac{{3(x - 2) - (3x + 1)}}{{{{(x - 2)}^2}}}\)
\(f'(x) = \frac{{ - 7}}{{{{(x - 2)}^2}}}\)
Vì \(f'(x) = \frac{{ - 7}}{{{{(x - 2)}^2}}}
Nên hàm số \(y = f(x) = \frac{{3x + 1}}{{x - 2}}\) không có cực trị.
Vận dụng (VD)
Trở lại bài toán Khởi động ban đầu bài học, hãy lập bảng biến thiên của hàm số \(y = C(x) = \frac{{30x}}{{{x^2} + 2}}\)trên khoảng \((0; + \infty )\)
Khi đó, cho biết hàm nồng độ thước trong máu :
a) Tăng trong khoảng thời gian nào
b) Đạt giá trị cực đại là bao nhiêu trong khoảng thời gian 6 phút sau khi tiêm
Bước 1: Tính \(C'(x)\)
Bước 2: Lập bảng biến thiên của hàm số
Bước 3: Tính hàm nồng độ thước trong máu tăng trong khoảng thời gian nào là tính hàm số \(C(x)\) tăng trong khoảng nào hay hàm số \(C(x)\)đồng biến trong khoảng nào
Bước 4: Nồng độ thước máu đạt cực đại là bao nhiêu trong 6 phút sau khi tiêm là giá trị cực đại của hàm số \(C(x)\) trong khoảng \((0;6)\)
Hàm số trên xác định trên R
Ta có: \(y’ = C'(x) = \frac{{30({x^2} + 2) - 30x.2x}}{{{{({x^2} + 2)}^2}}}\)
\( = \frac{{ - 30{x^2} + 60}}{{{{({x^2} + 2)}^2}}}\)
Xét \(y’ = 0\) \( \Rightarrow - 30{x^2} + 60 = 0\) \( \Leftrightarrow x = \sqrt 2 \)
Ta có bảng biến thiên:
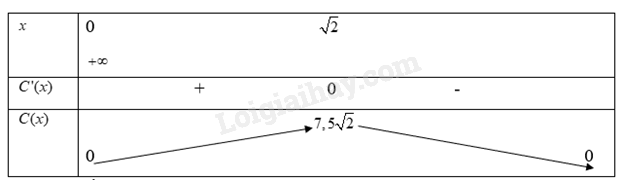
Từ bảng biến thiên, ta có :
a) Hàm số \(C(x)\)đồng biến trên khoảng \((0;7,5\sqrt 2 )\)hay nồng độ thước máu tăng từ sau khi tiêm đến \(7,5\sqrt 2 \)phút sau.
b) Hàm số \(C(x)\) đạt giá trị cực đại tại \(x = \sqrt 2 \)hay nồng độ thức máu đạt giá trị cực đại sau \(\sqrt 2 \) phút