Luyện tập (LT) 5
Cho hình lăng trụ ABC.A’B’C’ có \(\widehat {BAC} = \alpha \). Gọi M là một điểm bất kỳ thuộc cạnh bên AA’ (Hình 2.18).
a) Vẽ hai vectơ \(\overrightarrow {MP} \) và \(\overrightarrow {MQ} \) lần lượt bằng \(\overrightarrow {AB} \) và \(\overrightarrow {A’C’} \). ABC.MPQ có phải là hình lăng trụ không? Vì sao?
b) Trong mặt phẳng (MPQ), hãy xác định góc giữa hai vectơ \(\overrightarrow {MP} \), \(\overrightarrow {MQ} \) và so sánh góc đó với \(\alpha \).


- Sử dụng định nghĩa và tính chất của vectơ kết hợp với khái niệm và các tính chất của hình lăng trụ.
- Hình lăng trụ là hình đa diện bao gồm 2 đáy nằm trên hai mặt phẳng song song và là hai đa giác bằng nhau.

a) Ta có: \(\overrightarrow {MP} = \overrightarrow {AB} \) suy ra MP = AB và MP // AB (1)
Tương tự: \(\overrightarrow {MQ} = \overrightarrow {A’C’} \) suy ra MQ = A’C’ = AC và MQ // A’C’ // AC (2)
Từ (1) và (2) suy ra \(\Delta MPQ = \Delta ABC\).
ABC.MPQ có hai đáy song song và bằng nhau nên ABC.MPQ là hình lăng trụ.
b) Vì \(\Delta MPQ = \Delta ABC\) nên \(\widehat {PMQ} = \widehat {BAC} = \alpha \).
Mà góc giữa hai vectơ \(\overrightarrow {MP} \) và \(\overrightarrow {MQ} \) là góc\(\widehat {PMQ}\).
Vậy \(\widehat {(\overrightarrow {MP} ,\overrightarrow {MQ} )} = \alpha \).
Luyện tập (LT) 6
Cho hình lập phương \(ABCD.{A^\prime }{B^\prime }{C^\prime }{D^\prime }\). Tìm góc giữa vectơ \(\overrightarrow {{A^\prime }{C^\prime }} \) và
a) vecto \(\overrightarrow {AB} \);
b) vectơ \(\overrightarrow {AD} \);
c) vectơ \(\overrightarrow {{B^\prime }B} \).

Sử dụng các tính chất của hình lập phương để xác định góc của các vectơ.

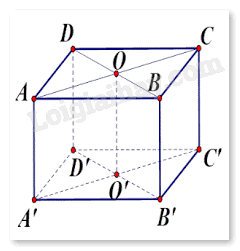
Gọi độ dài cạnh của hình lập phương là \(a\).
a) Tìm góc giữa vectơ \(\overrightarrow {{A^\prime }{C^\prime }} \) và vectơ \(\overrightarrow {AB} \):
Vì ABCD.A’B’C’D’ là hình lập phương nên \(\overrightarrow {{A^\prime }{C^\prime }} = \overrightarrow {AC} \).
Mà góc giữa \(\overrightarrow {AC} \) và \(\overrightarrow {AB} \) là \(\widehat {BAC}\) và vì ABCD là hình vuông nên \(\widehat {BAC} = 45^\circ \).
Suy ra \(\widehat {(\overrightarrow {A’C’} ,\overrightarrow {AB} )} = 45^\circ \).
b) Tìm góc giữa vectơ \(\overrightarrow {{A^\prime }{C^\prime }} \) và vectơ \(\overrightarrow {AD} \):
Tương tự như câu a ta có: \(\overrightarrow {{A^\prime }{C^\prime }} = \overrightarrow {AC} \).
Mà góc giữa \(\overrightarrow {AC} \) và \(\overrightarrow {AD} \) là \(\widehat {DAC}\) và vì ABCD là hình vuông nên \(\widehat {DAC} = 45^\circ \).
Suy ra \(\widehat {(\overrightarrow {A’C’}, \overrightarrow {AD} )} = 45^\circ \).
c) Tìm góc giữa vectơ \(\overrightarrow {{A^\prime }{C^\prime }} \) và vectơ \(\overrightarrow {{B^\prime }B} \):
Gọi O và O’ lần lượt là tâm của hình vuông ABCD và A’B’C’D’.
Vì O và O’ lần lượt là trung điểm của cạnh BD và B’D’ nên OO’ là đường trung bình của BB’D’D, suy ra \(\overrightarrow {B’B} = \overrightarrow {O’O} \).
Mà \(O’O \bot AC\) nên \(\widehat {(\overrightarrow {A’C’}, \overrightarrow {B’B} )} = 90^\circ \).
Hoạt động (HĐ) 6
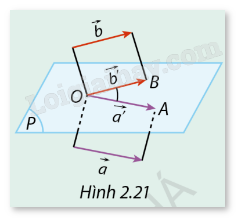
Trong không gian, cho hai vectơ \(\vec a,\vec b\) khác \(\vec 0\). Từ một điểm \(O\) tuỳ ý trong không gian, vẽ các vectơ \(\overrightarrow {{a^\prime }} ,\overrightarrow {{b^\prime }} \) sao cho \(\overrightarrow {{a^\prime }} = \vec a\), \(\overrightarrow {{b^\prime }} = \vec b\). (P) là mặt phẳng chứa giá của hai vectơ \(\overrightarrow {{a^\prime }} \) và \(\overrightarrow {{b^\prime }} \) (Hình 2.21).
a) Trong mặt phẳng \((P)\), hãy viết biểu thức tính \(\overrightarrow {{a^\prime }} \cdot \overrightarrow {{b^\prime }} \).
b) Hãy so sánh \(\overrightarrow {{a^\prime }} \cdot \overrightarrow {{b^\prime }} \) với \(|\vec a| \cdot |\vec b| \cdot \cos (\vec a,\vec b)\).

1. Sử dụng định nghĩa của tích vô hướng trong mặt phẳng \((P)\).
2. Sử dụng công thức của tích vô hướng để so sánh các biểu thức.

a) Trong mặt phẳng \((P)\), biểu thức tính \(\overrightarrow {{a^\prime }} \cdot \overrightarrow {{b^\prime }} \) được tính như sau:
\(\overrightarrow {{a^\prime }} \cdot \overrightarrow {{b^\prime }} = |\overrightarrow {{a^\prime }} | \cdot |\overrightarrow {{b^\prime }} | \cdot \cos \theta \)
trong đó \(\theta \) là góc giữa hai vectơ \(\overrightarrow {{a^\prime }} \) và \(\overrightarrow {{b^\prime }} \).
b) Vì \(\overrightarrow {{a^\prime }} = \vec a\) và \(\overrightarrow {{b^\prime }} = \vec b\), nên:
\(|\overrightarrow {{a^\prime }} | = |\vec a|,|\overrightarrow {{b^\prime }} | = |\vec b|\)
Do đó, ta có:
\(\overrightarrow {{a^\prime }} \cdot \overrightarrow {{b^\prime }} = |\vec a| \cdot |\vec b| \cdot \cos \theta \)
trong đó \(\theta \) là góc giữa hai vectơ \(\overrightarrow {{a^\prime }} \) và \(\overrightarrow {{b^\prime }} \).
Biểu thức này cho thấy rằng tích vô hướng của hai vectơ \(\overrightarrow {{a^\prime }} \) và \(\overrightarrow {{b^\prime }} \) trong mặt phẳng \((P)\) là bằng tích của độ lớn của hai vectơ \(\vec a\) và \(\vec b\) với cosin của góc giữa chúng. Vì vậy:
\(\overrightarrow {{a^\prime }} \cdot \overrightarrow {{b^\prime }} = |\vec a| \cdot |\vec b| \cdot \cos (\vec a,\vec b)\)
Điều này chứng minh rằng tích vô hướng của \(\overrightarrow {{a^\prime }} \) và \(\overrightarrow {{b^\prime }} \) trong mặt phẳng \((P)\) bằng tích vô hướng của \(\vec a\) và \(\vec b\).
Advertisements (Quảng cáo)
Luyện tập (LT) 7
Cho hình lập phương ABCD.A’B’C’D’ có cạnh bằng a. Hãy tính:
a) \(\overrightarrow {AB’} .\overrightarrow {A’C’} ;\)
b) \(\overrightarrow {AB’} .\overrightarrow {BD} ;\)
c) \(\overrightarrow {A’C’} .\overrightarrow {BB’} .\)

- Xác định độ dài của các vectơ và góc giữa chúng dựa vào tính chất của hình lập phương.
- Sử dụng công thức tích vô hướng \(\vec u \cdot \vec v = |\vec u||\vec v|\cos \theta \) để tính.

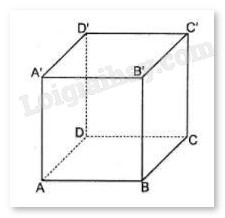
Gọi O và O’ lần lượt là tâm của hình vuông ABCD và A’B’C’D’.
a) Tính \(\overrightarrow {AB’} \cdot \overrightarrow {A’C’} \).
Độ dài của \(|\overrightarrow {AB’} | = |\overrightarrow {A’C’} | = a\sqrt 2 \) (vì AB’ và A’C’ là các cạnh đường chéo của các mặt bên của hình lập phương).
ABCD.A’B’C’D’ là hình lập phương nên \(\overrightarrow {{A^\prime }{C^\prime }} = \overrightarrow {AC} \).
Góc giữa \(\overrightarrow {AB’} \) và \(\overrightarrow {AC} \) là \({60^^\circ }\) vì chúng là hai cạnh của tam giác đều AB’C.
Do đó: \(\overrightarrow {AB’} .\overrightarrow {A’C’} = \left| {\overrightarrow {AB’} } \right|.\left| {\overrightarrow {A’C’} } \right|.\cos 60^\circ = a\sqrt 2 .a\sqrt 2 .\frac{1}{2} = {a^2}\).
b) Tính \(\overrightarrow {AB’} \cdot \overrightarrow {BD} \).
Độ dài của \(|\overrightarrow {AB’} | = a\sqrt 2 \) và \(|\overrightarrow {BD} | = a\sqrt 2 \) (cả hai đều là đường chéo của các mặt bên của hình lập phương).
Từ B vẽ một vectơ \(\overrightarrow {BE} \) bằng với vectơ \(\overrightarrow {AB’} \).
Vì D đối xứng với E qua tâm của hình vuông BB’C’C nên đường trung tuyến của tam giác cân BED có độ dài là \(\frac{{a\sqrt 2 }}{2}\).
Suy ra: \(\widehat {DBE} = 2\arccos \left( {\frac{{a\sqrt 2 }}{2}:a\sqrt 2 } \right) = 2\arccos \left( {\frac{1}{2}} \right) = 2.60^\circ = 120^\circ \).
Góc giữa \(\overrightarrow {AB’} \) và \(\overrightarrow {BD} \) cũng là góc giữa \(\overrightarrow {BE} \)và \(\overrightarrow {BD} \) là \(\widehat {DBE}\).
Do đó: \(\overrightarrow {AB’} .\overrightarrow {BD} = \left| {\overrightarrow {AB’} } \right|.\left| {\overrightarrow {BD} } \right|.\cos 120^\circ = a\sqrt 2 .a\sqrt 2 .\left( { - \frac{1}{2}} \right) = - {a^2}\).
c) Tính \(\overrightarrow {A’C’} \cdot \overrightarrow {BB’} \).
Độ dài của \(|\overrightarrow {A’C’} | = a\sqrt 2 \) và \(|\overrightarrow {BB’} | = a\).
ABCD.A’B’C’D’ là hình lập phương nên \(\overrightarrow {{A^\prime }{C^\prime }} = \overrightarrow {AC} ,\overrightarrow {BB’} = \overrightarrow {AA’} \).
Do \(\overrightarrow {AC} \) và \(\overrightarrow {AA’} \) vuông góc với nhau nên góc giữa \(\overrightarrow {A’C’} \) và \(\overrightarrow {BB’} \) Là 90°.
Suy ra: \(\overrightarrow {A’C’} .\overrightarrow {BB’} = \left| {\overrightarrow {A’C’} } \right|.\left| {\overrightarrow {BB’} } \right|.\cos 90^\circ = a\sqrt 2 .a.0 = 0\).
Luyện tập (LT) 8
Cho tứ diện ABCD có \(DA = DB = a\), \(BC = \frac{a}{2}\), \(AB \bot BC\) và \(\widehat {CBD} = {45^^\circ }\). Tính góc giữa hai vectơ \(\overrightarrow {AD} \) và \(\overrightarrow {BC} \).

- Tính tích vô hướng của \(\overrightarrow {BC} .\overrightarrow {BD} \), từ đó suy ra mối liên hệ với tích vô hướng của hai vectơ \(\overrightarrow {AD} \) và \(\overrightarrow {BC} \).
- Sử dụng công thức tích vô hướng giữa hai vectơ để tính cosin của góc giữa chúng:
\(\cos \theta = \frac{{\overrightarrow {AD} \cdot \overrightarrow {BC} }}{{|\overrightarrow {AD} | \times |\overrightarrow {BC} |}}\).

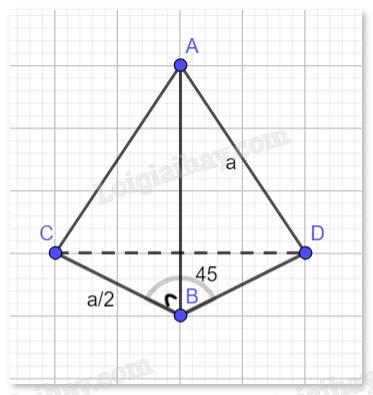
Ta có: \(\overrightarrow {BC} .\overrightarrow {BD} = BC.DB.\cos 45^\circ = \frac{a}{2}.a.\frac{{\sqrt 2 }}{2} = \frac{{{a^2}\sqrt 2 }}{4}\).
Mà: \(\overrightarrow {BC} .\overrightarrow {AD} = \overrightarrow {BC} .\overrightarrow {BD} + \overrightarrow {BC} .\overrightarrow {AB} \).
Suy ra: \(\overrightarrow {BC} .\overrightarrow {AD} = \frac{{{a^2}\sqrt 2 }}{4} + 0 = \frac{{{a^2}\sqrt 2 }}{4}\)(vì \(AB \bot BC\) nên \(\overrightarrow {BC} .\overrightarrow {AB} = 0\)).
Sử dụng công thức tích vô hướng giữa hai vectơ để tính cosin của góc giữa chúng:
\(\cos \theta = \frac{{\overrightarrow {AD} \cdot \overrightarrow {BC} }}{{|\overrightarrow {AD} | \times |\overrightarrow {BC} |}} = \frac{{\frac{{{a^2}\sqrt 2 }}{4}}}{{a.\frac{a}{2}}} = \frac{{\sqrt 2 }}{2}\).
Vậy góc giữa hai vectơ \(\overrightarrow {AD} \) và \(\overrightarrow {BC} \) là \(\arccos \left( {\frac{{\sqrt 2 }}{2}} \right) = 45^\circ \).
Luyện tập (LT) 9
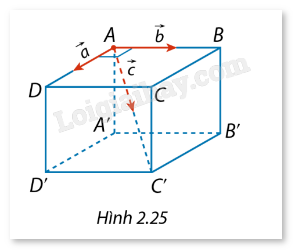
Một chất điểm ở vị trí đỉnh \(A\) của hình lập phương ABCD.A’B’C’D’. Chất điểm chịu tác động bởi ba lực \(\vec a\), \(\vec b\), \(\vec c\) lần lượt cùng hướng với \(\overrightarrow {AD} \), \(\overrightarrow {AB} \) và \(\overrightarrow {AC’} \) như Hình 2.25. Cường độ của các lực \(\vec a\), \(\vec b\) và \(\vec c\) tương ứng là \(10{\rm{ N}}\), \(10{\rm{ N}}\) và \(20{\rm{ N}}\). Tính cường độ hợp lực của \(\vec a\), \(\vec b\) và \(\vec c\) (làm tròn kết quả đến hàng phần mười).

- Sử dụng công thức quy tắc hình bình hành để tính tổng hợp lực của \(\vec a\), \(\vec b\).
\(F{}^\text{2}=\text{}{{F}_{1}}{}^\text{2}+{{F}_{2}}{}^\text{2}+2.{{}_{1}}.{{F}_{2}}.\cos \alpha \).
- Sau đó sử dụng kết quả vừa tính để tính tổng hợp lực với \(\vec c\).

Vì ABCD.A’B’C’D’ là hình lập phương nên góc giữa \(\overrightarrow {AD} \)và \(\overrightarrow {AB} \) là 90°.
Suy ra lực \(\vec a\) vuông góc với \(\vec b\). Vậy hợp lực của hai lực \(\vec a\) và \(\vec b\) là:
\(\overrightarrow {{F_{ab}}} = \overrightarrow {{F_a}} + \overrightarrow {{F_b}} \Rightarrow {F_{ab}} = \sqrt {{F_a}^2 + {F_b}^2} = \sqrt {{{10}^2} + {{10}^2}} = 10\sqrt 2 N\).
Vì tam giác ACC’ là tam giác vuông tại C nên ta có:
\(AC’ = \sqrt {A{C^2} + CC{‘^2}} = \sqrt {A{C^2} + \frac{{A{C^2}}}{2}} = AC\sqrt {\frac{3}{2}} \) (vì CC’ là cạnh bên của hình lập phương còn AC là đường chéo của mặt bên nên \(CC’ = \frac{{AC}}{{\sqrt 2 }}\)).
\(\cos \widehat {CAC’} = \frac{{AC}}{{AC’}} = \frac{{AC}}{{AC\sqrt {\frac{3}{2}} }} = \frac{{\sqrt 6 }}{3}\).
Hợp lực của \(\vec a\), \(\vec b\) và \(\vec c\) là:
\(F = \sqrt {{F_{ab}}^2 + F_c^2 + 2.{F_{ab}}.{F_c}.\cos \widehat {CAC’}} = \sqrt {{{\left( {10\sqrt 2 } \right)}^2} + {{20}^2} + 2.10\sqrt 2 .20.\frac{{\sqrt 6 }}{3}} = 32,6N\).
