
Giả sử hàm cầu đối với một loại hàng hóa được cho bởi công thức \(p = \frac{{354}}{{1 + 0,01x}},x \ge 0\), trong đó p là giá bán (nghìn đồng) của mỗi đơn vị sản phẩm và x là số lượng đơn vị sản phẩm đã bán.a) Tìm công thức tính x như là hàm số của p. Tìm tập xác định của hàm số này. Tính số đơn vị sản phẩm đã bán khi giá bán của mỗi đơn vị sản phẩm là 240 nghìn đồng.b) Khảo sát sự biến thiên và vẽ đồ thị của hàm số \(x = x\left( p \right)\). Từ đồ thị đã vẽ, hãy cho biết:- Số lượng đơn vị sản phẩm bán được sẽ thay đổi thế nào khi giá bán p tăng;- Ý nghĩa thực tiễn của giới hạn \(\mathop {\lim }\limits_{p \to {0^ + }} x\left( p \right)\).

Sử dụng kiến thức về sơ đồ khảo sát hàm số phân thức để khảo sát và vẽ đồ thị hàm số:
Sơ đồ khảo sát hàm số phân thức
1. Tìm tập xác định của hàm số.
2. Khảo sát sự biến thiên của hàm số:
+ Tính đạo hàm y’. Tìm các điểm tại đó y’ bằng 0 hoặc đạo hàm không tồn tại.
+ Xét dấu y’ để chỉ ra các khoảng đơn điệu của hàm số.
+ Tìm cực trị của hàm số.
+ Tìm các giới hạn tại vô cực, giới hạn vô cực và tìm tiệm cận của đồ thị hàm số.
+ Lập bảng biến thiên của hàm số.
3. Vẽ đồ thị của hàm số dựa vào bảng biến thiên

a) Tìm công thức tính x như là hàm số của p. Tìm tập xác định của hàm số này. Tính số đơn vị sản phẩm đã bán khi giá bán của mỗi đơn vị sản phẩm là 240 nghìn đồng.
Vì \(p = \frac{{354}}{{1 + 0,01x}} \Rightarrow p\left( {1 + 0,01x} \right) = 354 \Rightarrow p + 0,01px = 354 \Rightarrow x = \frac{{354 - p}}{{0,01p}}\)
Tập xác định của hàm số là: \(\left( {0;354} \right]\)
Với \(p = 240\) ta có: \(x = \frac{{354 - 240}}{{0,01.240}} = 47,5\)
Vậy với giá bán mỗi đơn vị sản phẩm là 240 nghìn đồng thì bán được 47,5 đơn vị sản phẩm.
Advertisements (Quảng cáo)
b) Khảo sát sự biến thiên của hàm số: \(x = x\left( p \right) = \frac{{354 - p}}{{0,01p}}\)
1. Tập xác định của hàm số: \(\left( {0;354} \right]\)
2. Sự biến thiên:
Ta có: \(x’\left( p \right) = \frac{{ - 3,54}}{{{{\left( {0,01p} \right)}^2}}} < 0\) với mọi \(p \in \left( {0;354} \right]\).
Hàm số nghịch biến trên khoảng \(\left( {0;354} \right)\).
Hàm số không có cực trị.
Giới hạn: \(\mathop {\lim }\limits_{p \to {0^ + }} x\left( p \right) = \mathop {\lim }\limits_{p \to {0^ + }} \frac{{354 - p}}{{0,01p}} = + \infty \)
Do đó, đồ thị hàm số \(x = x\left( p \right) = \frac{{354 - p}}{{0,01p}}\) với \(p \in \left( {0;354} \right]\) nhận đường thẳng \(p = 0\) làm tiệm cận đứng.
Bảng biến thiên:
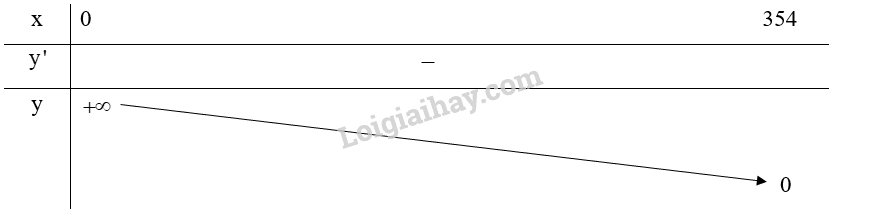
3. Đồ thị:
Ta có: \(f\left( p \right) = 0 \Leftrightarrow \frac{{354 - p}}{{0,01p}} = 0 \Leftrightarrow p = 354\)
Đồ thị hàm số \(x = f\left( p \right) = \frac{{354 - p}}{{0,01p}}\) cắt trục hoành tại điểm (354; 0).
Đồ thị hàm số \(x = f\left( p \right) = \frac{{354 - p}}{{0,01p}}\) đi qua các điểm (300; 18); (200; 77).
Đồ thị hàm số \(x = f\left( p \right) = \frac{{354 - p}}{{0,01p}}\) với \(p \in \left( {0;354} \right]\) là đường màu xanh:
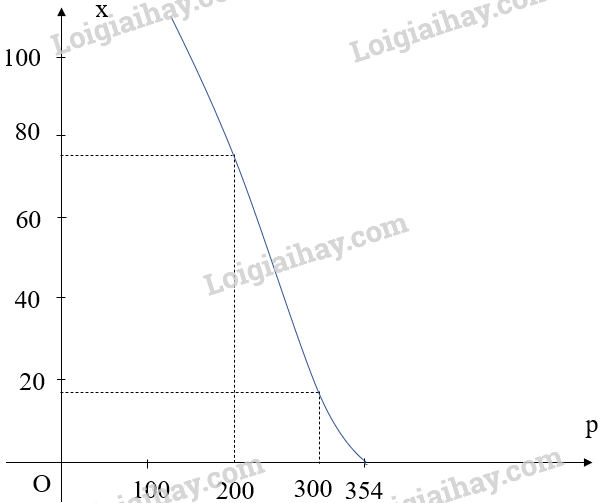
- Số lượng đơn vị sản phẩm bán sẽ giảm đi khi giá bán tăng, và sẽ không bán được sản phẩm nào nếu giá bán là 354 nghìn đồng
- Ý nghĩa thực tiễn của giới hạn \(\mathop {\lim }\limits_{p \to {0^ + }} x\left( p \right)\): Vì \(\mathop {\lim }\limits_{p \to {0^ + }} x\left( p \right) = + \infty \) nên giá bán càng thấp thì số lượng đơn vị sản phẩm sẽ bán được càng nhiều.
