
Cho tứ diện ABCD. Lấy G là trọng tâm của tam giác BCD. Khẳng định nào sau đây là sai? A. \(\overrightarrow {BG} + \overrightarrow {CG} + \overrightarrow {DG} = \overrightarrow 0 \).B. \(\overrightarrow {AB} + \overrightarrow {AC} + \overrightarrow {AD} = 3\overrightarrow {AG} \).C. \(\overrightarrow {BC} + \overrightarrow {BD} = 3\overrightarrow {BG} \).D. \(\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} + \overrightarrow {GD} = \overrightarrow 0 \).

Sử dụng kiến thức về trọng tâm của tam giác để chứng minh: Nếu G là trọng tâm của tam giác BCD thì \(\overrightarrow {GB} + \overrightarrow {GC} + \overrightarrow {GD} = \overrightarrow 0 \).
Sử dụng kiến thức về trung điểm của đoạn thẳng để chứng minh: Nếu I là trung điểm của đoạn thẳng AB, với điểm M tùy ý ta có: \(\overrightarrow {MA} + \overrightarrow {MB} = 2\overrightarrow {MI} \).
Sử dụng kiến thức về quy tắc ba điểm để chứng minh: Nếu A, B, C là ba điểm bất kì thì \(\overrightarrow {AB} + \overrightarrow {BC} = \overrightarrow {AC} \).

Advertisements (Quảng cáo)
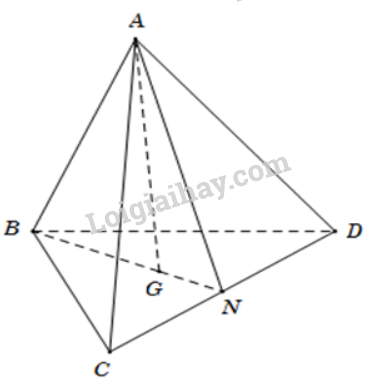
Vì G là trọng tâm của tam giác BCD nên \(\overrightarrow {GB} + \overrightarrow {GC} + \overrightarrow {GD} = \overrightarrow 0 \Rightarrow \overrightarrow {BG} + \overrightarrow {CG} + \overrightarrow {DG} = \overrightarrow 0 \), do đó A đúng.
Vì \(\overrightarrow {AB} + \overrightarrow {AC} + \overrightarrow {AD} = \overrightarrow {AG} + \overrightarrow {GB} + \overrightarrow {AG} + \overrightarrow {GC} + \overrightarrow {AG} + \overrightarrow {GD} = 3\overrightarrow {AG} + \left( {\overrightarrow {GB} + \overrightarrow {GC} + \overrightarrow {GD} } \right) = 3\overrightarrow {AG} \), do đó B đúng.
Gọi N là trung điểm của CD, khi đó, \(\overrightarrow {BC} + \overrightarrow {BD} = 2\overrightarrow {BN} = 2.\frac{3}{2}\overrightarrow {BG} = 3\overrightarrow {BG} \) nên C đúng.
Ta có: \(\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} + \overrightarrow {GD} = \overrightarrow {GA} + \overrightarrow 0 = \overrightarrow {GA} \) nên D sai.
Chọn D
