Hoạt động1
Trả lời câu hỏi Hoạt động 1 trang 20 SGK Toán 12 Kết nối tri thức
Cho hàm số \(y = f\left( x \right) = \frac{{2x + 1}}{x}\) có đồ thị (C). Với \(x > 0\), xét điểm M (x; f(x)) thuộc (C). Gọi H là hình chiếu vuông góc của M trên đường thẳng \(y = 2\) (H.1.19).
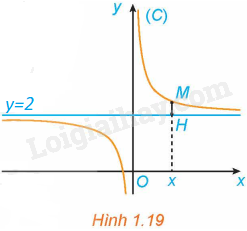
a) Tính khoảng cách MH.
b) Có nhận xét gì về khoảng cách MH khi \(x \to + \infty \)?

Sử dụng kiến thức về giới hạn của hàm số để tính.

a) Ta có: \(M\left( {x;\frac{{2x + 1}}{x}} \right)\); \(H\left( {x;2} \right)\).
Do đó, \(MH = \sqrt {{{\left( {x - x} \right)}^2} + {{\left( {2 - \frac{{2x + 1}}{x}} \right)}^2}} = \sqrt {{{\left( {\frac{{2x - 2x - 1}}{x}} \right)}^2}} = \frac{1}{x}\) (do \(x > 0\))
b) Ta có: \(\mathop {\lim }\limits_{x \to + \infty } \frac{1}{x} = 0\). Do đó, khi \(x \to + \infty \) thì \(MH \to 0\).
Luyện tập1
Trả lời câu hỏi Luyện tập 1 trang 21 SGK Toán 12 Kết nối tri thức
Tìm tiệm cận ngang của đồ thị hàm số \(y = f\left( x \right) = \frac{{2x - 1}}{{x - 1}}\).

Advertisements (Quảng cáo)
Sử dụng kiến thức về khái niệm tiệm cận ngang của đồ thị hàm số để tìm tiệm cận ngang: Đường thẳng \(y = {y_0}\) gọi là đường tiệm cận ngang (gọi tắt là tiệm cận ngang) của đồ thị hàm số \(y = f\left( x \right)\) nếu \(\mathop {\lim }\limits_{x \to + \infty } f\left( x \right) = {y_0}\) hoặc \(\mathop {\lim }\limits_{x \to - \infty } f\left( x \right) = {y_0}\).

Ta có: \(\mathop {\lim }\limits_{x \to + \infty } \frac{{2x - 1}}{{x - 1}} = \mathop {\lim }\limits_{x \to + \infty } \frac{{2 - \frac{1}{x}}}{{1 - \frac{1}{x}}} = 2;\mathop {\lim }\limits_{x \to - \infty } \frac{{2x - 1}}{{x - 1}} = \mathop {\lim }\limits_{x \to - \infty } \frac{{2 - \frac{1}{x}}}{{1 - \frac{1}{x}}} = 2\).
Do đó, tiệm cận ngang của đồ thị hàm số \(y = f\left( x \right) = \frac{{2x - 1}}{{x - 1}}\) là \(y = 2\).
Vận dụng1
Trả lời câu hỏi Vận dụng 1 trang 21 SGK Toán 12 Kết nối tri thức
Giải bài toán trong tình huống mở đầu.
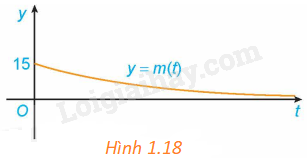
Giả sử khối lượng còn lại của một chất phóng xạ (gam) sau t ngày phân rã được cho bởi hàm số \(m\left( t \right) = 15{e^{ - 0,012t}}\). Khối lượng m(t) thay đổi ra sao khi \(t \to + \infty \)? Điều này thể hiện trên Hình 1.18 như thế nào?

Sử dụng kiến thức về khái niệm tiệm cận ngang của đồ thị hàm số để tìm tiệm cận ngang: Đường thẳng \(y = {y_0}\) gọi là đường tiệm cận ngang (gọi tắt là tiệm cận ngang) của đồ thị hàm số \(y = f\left( x \right)\) nếu \(\mathop {\lim }\limits_{x \to + \infty } f\left( x \right) = {y_0}\) hoặc \(\mathop {\lim }\limits_{x \to - \infty } f\left( x \right) = {y_0}\).

Ta có: \(\mathop {\lim }\limits_{t \to + \infty } m\left( t \right) = \mathop {\lim }\limits_{t \to + \infty } 15{e^{ - 0,012t}} = \mathop {\lim }\limits_{t \to + \infty } \frac{{15}}{{{e^{0,012t}}}} = 0\)
Do đó, \(m\left( t \right) \to 0\) khi \(t \to + \infty \).
Trong hình 1.18, khi \(t \to + \infty \) thì m(t) càng gần trục hoành Ot (nhưng không chạm trục Ot).
