Câu hỏi/bài tập:
Một công ty dược phẩm muốn so sánh tác dụng điều trị bệnh X của hai loại thuốc M và N. Công ty đã tiến hành thử nghiệm với 4 000 bệnh nhân mắc bệnh X trong đó 2 400 bệnh nhân dùng thuốc M, 1 600 bệnh nhân còn lại dùng thuốc N. Kết quả được cho trong bảng dữ liệu thống kê \(2 \times 2\) như sau:
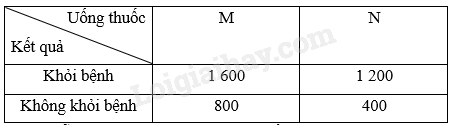
Chọn ngẫu nhiên một bệnh nhân trong số 4 000 bệnh nhân thử nghiệm sau khi uống thuốc. Tính xác suất để bệnh nhân đó
a) uống thuốc M, biết rằng bệnh nhân đó khỏi bệnh;
b) uống thuốc N, biết rằng bệnh nhân đó không khỏi bệnh.

Sử dụng kiến thức về công thức tính xác suất có điều kiện để tính: Cho hai biến cố A và B bất kì, với \(P\left( B \right) > 0\). Khi đó, \(P\left( {A|B} \right) = \frac{{P\left( {AB} \right)}}{{P\left( B \right)}}\).

Không gian mẫu \(\Omega \) là tập hợp gồm 4 000 bệnh nhân thử nghiệm nên \(n\left( \Omega \right) = 4000\)
Advertisements (Quảng cáo)
a) Gọi A là biến cố: “Người đó uống thuốc M”, B là biến cố “Người đó khỏi bệnh”
Khi đó biến cố AB là: “Người đó uống thuốc M và khỏi bệnh”
Ta có: \(1600 + 1200 = 2800\) người khỏi bệnh nên \(n\left( B \right) = 3800\). Do đó, \(P\left( B \right) = \frac{{2800}}{{4000}}\)
Trong số những người khỏi bệnh, có 1 600 người uống thuốc M nên \(n\left( {AB} \right) = 1\;600\)
Do đó, \(P\left( {AB} \right) = \frac{{1600}}{{4000}}\). Vậy \(P\left( {A|B} \right) = \frac{{P\left( {AB} \right)}}{{P\left( B \right)}} = \frac{{1600}}{{2800}} = \frac{4}{7}\)
b) Gọi A là biến cố: “Người đó uống thuốc N”, B là biến cố “Người đó không khỏi bệnh”.
Khi đó biến cố AB là: “Người đó uống thuốc N và không khỏi bệnh”
Ta có: \(800 + 400 = 1200\) người không khỏi bệnh nên \(n\left( B \right) = 1200\). Do đó, \(P\left( B \right) = \frac{{1200}}{{4000}}\)
Trong số những người không khỏi bệnh, có 400 người uống thuốc N nên \(n\left( {AB} \right) = 400\)
Do đó, \(P\left( {AB} \right) = \frac{{400}}{{4000}}\). Vậy \(P\left( {A|B} \right) = \frac{{P\left( {AB} \right)}}{{P\left( B \right)}} = \frac{{400}}{{1200}} = \frac{1}{3}\)
