Câu hỏi/bài tập:
Ta biết rằng hàm cầu liên quan đến giá p của một sản phẩm với nhu cầu của người tiêu dùng, hàm cung liên quan đến giá p của sản phẩm với mức độ sẵn sàng cung cấp sản phẩm của nhà sản xuất. Điểm cắt nhau \(\left( {{x_o};{p_o}} \right)\) của đồ thị hàm cầu \(p = D\left( x \right)\) và đồ thị hàm cung \(p = S\left( x \right)\) được gọi là điểm cân bằng.
Các nhà kinh tế gọi diện tích của hình giới hạn bởi đồ thị hàm cầu, đường ngang \(p = {p_o}\) và đường thẳng đứng \(x = 0\) là thặng dư tiêu dùng. Tương tự, diện tích của hình giới hạn bởi đồ thị của hàm cung, đường nằm ngang \(p = {p_o}\) và đường thẳng đứng \(x = 0\) được gọi là thặng dư sản xuất, như trong Hình 4.19.
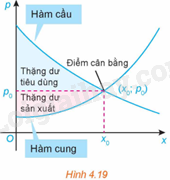
(Theo R. Larson, Brief Calculus: An Applied Approach, 8th edition, Cengage Learning, 2009)
Giả sử hàm cung và hàm cầu của một loại sản phẩm được mô hình hóa bởi:
Hàm cầu: \(p = - 0,36x + 9\) và hàm cung: \(p = 0,14x + 2\), trong đó x là số đơn vị sản phẩm. Tìm thặng dư tiêu dùng và thặng dư sản xuất cho sản phẩm này.

Sử dụng kiến thức về diện tích hình phẳng giới hạn bởi hai đồ thị hàm số và đường thẳng \(x = a,x = b\) để tính: Diện tích S của hình phẳng giới hạn đồ thị của hai hàm số f(x), g(x) liên tục trên đoạn [a; b] và hai đường thẳng \(x = a,x = b\), được tính bằng công thức \(S = \int\limits_a^b {\left| {f\left( x \right) - g\left( x \right)} \right|dx} \).

Gọi điểm M là giao điểm của hàm cầu \(p = - 0,36x + 9\) và hàm cung \(p = 0,14x + 2\)
Advertisements (Quảng cáo)
Khi đó, phương trình hoành độ giao điểm của hàm cầu và hàm cung là:
\( - 0,36x + 9 = 0,14x + 2\), suy ra \(x = 14\) nên \(p = - 0,36.14 + 9 = \frac{{99}}{{25}}\). Do đó, \(M\left( {14;\frac{{99}}{{25}}} \right)\)
Đồ thị hàm số \(p = - 0,36x + 9\) đi qua điểm \(M\left( {14;\frac{{99}}{{25}}} \right)\) và điểm N(0 ;9)
Đồ thị hàm số \(p = 0,14x + 2\) đi qua điểm \(M\left( {14;\frac{{99}}{{25}}} \right)\) và điểm P(0; 2)
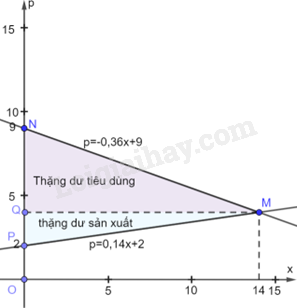
Diện tích hình giới hạn bởi đồ thị hàm số \(p = - 0,36x + 9\), trục hoành và hai đường thẳng \(x = 0,x = 14\) là: \({S_1} = \int\limits_0^{14} {\left| { - 0,36x + 9} \right|dx} = \int\limits_0^{14} {\left( { - 0,36x + 9} \right)dx} = \left( { - 0,18{x^2} + 9x} \right)\left| \begin{array}{l}14\\0\end{array} \right.\)
\( = - 0,{18.14^2} + 9.14 = 90,72\)
Diện tích hình giới hạn bởi đồ thị hàm số \(p = 0,14x + 2\), trục hoành và hai đường thẳng \(x = 0,x = 14\) là:
\({S_2} = \int\limits_0^{14} {\left| {0,14x + 2} \right|dx} = \int\limits_0^{14} {\left( {0,14x + 2} \right)dx} = \left( {0,07{x^2} + 2x} \right)\left| \begin{array}{l}14\\0\end{array} \right.\)\( = 0,{07.14^2} + 2.14 = 41,72\)
Thặng dư tiêu dùng cho sản phẩm này là: \({S_1} - OQ.QM = 90,72 - 14.\frac{{99}}{{25}} = 35,28\)
Thặng dư sản xuất cho sản phẩm này là: \(OQ.OM - {S_2} = 14.\frac{{99}}{{25}} - 41,72 = 13,72\)
