Câu hỏi/bài tập:
a) Tính đạo hàm của các hàm số sau và nêu kết quả tương ứng vào bảng dưới đây.
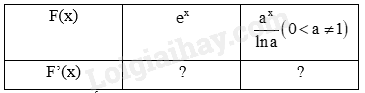
b) Sử dụng kết quả ở câu a, tìm nguyên hàm của các hàm số cho trong bảng dưới đây.


a) Sử dụng kiến thức về đạo hàm của hàm số mũ để tính: \(\left( {{e^x}} \right)’ = {e^x},\left( {{a^x}} \right)’ = {a^x}.\ln a\)
Advertisements (Quảng cáo)
b) Sử dụng kiến thức về khái niệm nguyên hàm của một hàm số để tính: Cho hàm số f(x) xác định trên một khoảng K (hoặc một đoạn, hoặc một nửa khoảng). Hàm số F(x) được gọi là một nguyên hàm của hàm số f(x) trên K nếu \(F’\left( x \right) = f\left( x \right)\) với mọi x thuộc K.
Sử dụng kiến thức về họ nguyên hàm của một hàm số để tính: Để tìm nguyên hàm của hàm số f(x) trên K, ta chỉ cần tìm một nguyên hàm F(x) của f(x) trên K và khi đó \(\int {f\left( x \right)dx = F\left( x \right) + C} \), C là hằng số.

a)
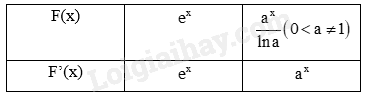
b)

