Câu hỏi/bài tập:
Tính diện tích hình phẳng giới hạn bởi parabol \(y = {x^2} - 4\), trục hoành và hai đường thẳng \(x = 0,x = 3\) (H.4.15).
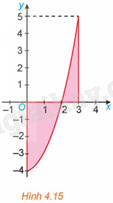

Sử dụng kiến thức về ứng dụng tích phân để tính diện tích hình phẳng để tính: Diện tích S của hình phẳng giới hạn bởi đồ thị của hàm số f(x) liên tục, trục hoành và hai đường thẳng \(x = a,x = b\left( {a < b} \right)\), được tính bằng công thức \(S = \int\limits_a^b {\left| {f\left( x \right)} \right|dx} \).
Advertisements (Quảng cáo)

Diện tích hình phẳng cần tính là:
\(S = \int\limits_0^3 {\left| {{x^2} - 4} \right|dx} = \int\limits_0^2 {\left| {{x^2} - 4} \right|dx} + \int\limits_2^3 {\left| {{x^2} - 4} \right|dx} = - \int\limits_0^2 {\left( {{x^2} - 4} \right)dx} + \int\limits_2^3 {\left( {{x^2} - 4} \right)dx} \)
\( = - \left( {\frac{{{x^3}}}{3} - 4x} \right)\left| \begin{array}{l}2\\0\end{array} \right. + \left( {\frac{{{x^3}}}{3} - 4x} \right)\left| \begin{array}{l}3\\2\end{array} \right. = - \left( {\frac{{{2^3}}}{3} - 4.2} \right) + \left( {\frac{{{3^3}}}{3} - 4.3 - \frac{{{2^3}}}{3} + 4.2} \right) = \frac{{16}}{3} + \frac{7}{3} = \frac{{23}}{3}\)
