Advertisements (Quảng cáo)
a) Hợp thành của hai phép đối xứng qua hai mặt phẳng song song (P) và (Q) là một phép tịnh tiến ;
b) Hợp thành của hai phép đối xứng qua hai mặt phẳng (P) và (Q) vuông góc với nhau là một phép đối xứng qua đường thẳng.. Bài 10 trang 15 SGK Hình học 12 Nâng cao - Bài 2. Phép đối xứng qua mặt phẳng và sự bằng nhau của các khối đa diện
Bài 10. Chứng minh rằng :
a) Hợp thành của hai phép đối xứng qua hai mặt phẳng song song \((P)\) và \((Q)\) là một phép tịnh tiến ;
b) Hợp thành của hai phép đối xứng qua hai mặt phẳng \((P)\) và \((Q)\) vuông góc với nhau là một phép đối xứng qua đường thẳng.
a)
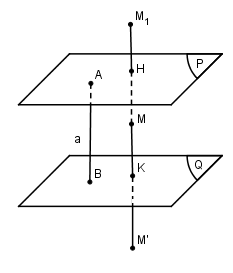
Lấy hai điểm \(A\) và \(B\) lần lượt nằm trên \((P)\) và \((Q)\) sao cho \(AB \bot \left( P \right)\). Với một điểm \(M\) bất kì, ta gọi \({M_1}\) là điểm đối xứng với \(M\) qua mp\((P)\) và \(M’\) là điểm đối xứng với \({M_1}\) qua mp\((Q)\).
Như vậy \(M’\) là ảnh của \(M\) qua phép hợp thành của phép đối xứng qua mp\((P)\) và phép đối xứng qua mp\((Q)\).
Gọi \(H\) và \(K\) lần lượt là trung điểm của \(M{M_1}\) và \({M_1}M’\) thì ta có:
\(\overrightarrow {MM’} = \overrightarrow {M{M_1}} + \overrightarrow {{M_1}M’} = 2\left( {\overrightarrow {H{M_1}} + \overrightarrow {{M_1}K} } \right) = 2\overrightarrow {HK} = 2\overrightarrow {AB} \)
Như vậy phép hợp thành nói trên chính là phép tịnh tiến theo vectơ \(2\overrightarrow {AB} \).
b)
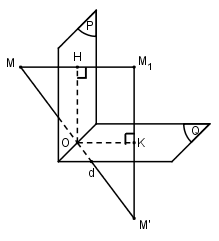
Giả sử \(\left( P \right) \bot \left( Q \right)\) và \(d = \left( P \right) \cap \left( Q \right)\)
Gọi \({M_1}\) là điểm đối xứng của \(M\) qua \((P)\) và \(H\) là trung điêm của \(M{M_1}\).
Gọi \(M’\) là điểm đối xứng của \({M_1}\) qua \((Q)\) và \(K\) là trung điểm của \({M_1}M’\)
Gọi \(O\) là giao điểm của \(\left( {M{M_1}M’} \right)\) với \(d\)
Ta có \(\left( {M{M_1}M’} \right) \bot \left( P \right)\,\,;\,\,\left( {M{M_1}M’} \right) \bot \left( Q \right) \Rightarrow \left( {M{M_1}M’} \right) \bot d\)
Ta có \(OH{M_1}K\) là hình chữ nhật và
\(\overrightarrow {OM} + \overrightarrow {OM’} = \overrightarrow {OH} + \overrightarrow {HM} + \overrightarrow {OK} + \overrightarrow {KM’} = \left( {\overrightarrow {OH} + \overrightarrow {OK} } \right) + \left( {\overrightarrow {{M_1}H} + \overrightarrow {{M_1}K} } \right) = \overrightarrow {O{M_1}} + \overrightarrow {{M_1}O} = \overrightarrow 0 \)
Suy ra \(O\) là trung điểm của \(MM’\), mặt khác \(MM’ \bot d\). Vậy phép hợp thành của phép đối xứng qua mp\((P)\) và phép đối xứng qua mp\((Q)\) với \(\left( P \right) \bot \left( Q \right)\) là phép đối xứng qua đường thẳng \(d\).
