Bài 20.Tính
a) \(\int\limits_0^\pi {5{{\left( {5 - 4\cos t} \right)}^{{1 \over 4}}}} \sin tdt;\)
b) \(\int\limits_0^{\sqrt 3 } {{{{x^3}dx} \over {\sqrt {{x^2} + 1} }}} .\)

a) Đặt \(u = 5 - 4\cos t \Rightarrow du = 4\sin tdt \Rightarrow \sin tdt = {1 \over 4}du\)
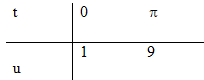
Advertisements (Quảng cáo)
\(\int\limits_0^\pi {5{{\left( {5 - 4\cos t} \right)}^{{1 \over 4}}}} \sin tdt = {5 \over 4}\int\limits_1^9 {{u^{{1 \over 4}}}du = \left. {{u^{{5 \over 4}}}} \right|} _1^9 = {9^{{5 \over 4}}} - 1\)
b) Đặt \(u = \sqrt {{x^2} + 1} \Rightarrow {u^2} = {x^2} + 1 \Rightarrow udu = xdx \Rightarrow {x^3}dx = {x^2}.xdx = \left( {{u^2} - 1} \right)udu\)
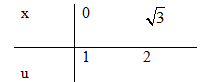
\(\int\limits_0^{\sqrt 3 } {{{{x^3}dx} \over {\sqrt {{x^2} + 1} }}} = \int\limits_1^2 {{{\left( {{u^2} - 1} \right)u} \over u}} du\)
\(\int\limits_1^2 {\left( {{u^2} - 1} \right)du} = \left. {\left( {{{{u^3}} \over 3} - u} \right)} \right|_1^2 = {4 \over 3}\)
