Bài 34. Tìm các đường tiệm cận của đồ thị hàm số sau:
a) \(y = {{x - 2} \over {3x + 2}}\) b) \(y = {{ - 2x - 2} \over {x + 3}}\)
c) \(y = x + 2 - {1 \over {x - 3}}\) d) \(y = {{{x^2} - 3x + 4} \over {2x + 1}}\)
e) \(y = {{x + 2} \over {{x^2} - 1}}\) f) \(y = {x \over {{x^3} + 1}}\)
Gỉải
a) TXĐ: \(D = \mathbb R\backslash \left\{ { - {2 \over 3}} \right\}\)
Vì \(\mathop {\lim }\limits_{x \to + \infty } y = \mathop {\lim }\limits_{x \to + \infty } {{x + 2} \over {3x + 2}} = \mathop {\lim }\limits_{x \to + \infty } {{1 - {2 \over x}} \over {3 + {2 \over x}}} = {1 \over 3}\) và \(\mathop {\lim }\limits_{x \to - \infty } y = {1 \over 3}\) nên đường thẳng \(y = {1 \over 3}\) là đường tiệm cận ngang của đồ thị.
Vì \(\mathop {\lim }\limits_{x \to {{\left( { - {2 \over 3}} \right)}^ + }} y = - \infty \) \(\mathop {\lim }\limits_{x \to {{\left( { - {2 \over 3}} \right)}^ - }} y = + \infty \); nên đường thẳng \(x = - {2 \over 3}\) là tiệm cận đứng của đồ thị.
b) TXĐ: \(D =\mathbb R\backslash \left\{ { - 3} \right\}\)
Vì \(\mathop {\lim }\limits_{x \to + \infty } y = \mathop {\lim }\limits_{x \to + \infty } {{ - 2 - {2 \over x}} \over {1 + {3 \over x}}} = - 2\) và \(\mathop {\lim }\limits_{x \to - \infty } y = - 2\) nên đường thẳng \(y = - 2\) là tiệm cận ngang của đồ thị.
Vì \(\mathop {\lim }\limits_{x \to {{\left( { - 3} \right)}^ + }} y = + \infty \) và \(\mathop {\lim }\limits_{x \to {{\left( { - 3} \right)}^ - }} y = - \infty \) nên đường thẳng \(x = - 3\) là tiệm cận đứng của đồ thị.
c) TXĐ: \(D =\mathbb R\backslash \left\{ 3 \right\}\)
Vì \(\mathop {\lim }\limits_{x \to {3^ + }} y = - \infty \) và \(\mathop {\lim }\limits_{x \to {3^ - }} y = + \infty \) nên đường thẳng \(x = 3\) là tiệm cận đứng của đồ thị.
Ta có: \(\mathop {\lim }\limits_{x \to + \infty } \left[ {y - \left( {x + 2} \right)} \right] = \mathop {\lim }\limits_{x \to + \infty } {{ - 1} \over {x - 3}} = 0\) và \(\mathop {\lim }\limits_{x \to - \infty } \left[ {y - \left( {x + 2} \right)} \right] = \mathop {\lim }\limits_{x \to - \infty } {{ - 1} \over {x - 3}} = 0\) nên đường thẳng \(y = x + 2\) là tiệm cận xiên của đồ thị.
d) TXĐ: \(D =\mathbb R\backslash \left\{ { - {1 \over 2}} \right\}\)
Vì \(\mathop {\lim }\limits_{x \to {{\left( { - {1 \over 2}} \right)}^ + }} y = + \infty \) và \(\mathop {\lim }\limits_{x \to {{\left( { - {1 \over 2}} \right)}^ - }} y = - \infty \) nên đường thẳng \(x = - {1 \over 2}\) là tiệm cận đứng của đồ thị.
Tiệm cận xiên có dạng \(y = ax + b\)
Advertisements (Quảng cáo)
\(\eqalign{
& a = \mathop {\lim }\limits_{x \to \pm \infty } {y \over x} = \mathop {\lim }\limits_{x \to \pm \infty } {{{x^2} - 3x + 4} \over {x\left( {2x + 1} \right)}} = {1 \over 2} \cr
& b = \mathop {\lim }\limits_{x \to \pm \infty } \left( {y - {x \over 2}} \right) = \mathop {\lim }\limits_{x \to \pm \infty } \left( {{{{x^2} - 3x + 4} \over {2x + 1}} - {x \over 2}} \right) = \mathop {\lim }\limits_{x \to \pm \infty } {{ - 7x + 8} \over {2\left( {2x + 1} \right)}} = - {7 \over 4} \cr} \)
\(\mathop {\lim }\limits_{x \to {{\left( { - 1} \right)}^ - }} y = + \infty \)
Đường thẳng \(y = {x \over 2} - {7 \over 4}\) là tiệm cận xiên của đồ thị (khi \(x \to + \infty \) và \(x \to - \infty \)).
Cách khác:
Ta có: \(y = {1 \over 2}.{{{x^2} - 3x + 4} \over {x + {1 \over 2}}} = {1 \over 2}\left( {x - {7 \over 2} + {{23} \over {4\left( {x + {1 \over 2}} \right)}}} \right)\)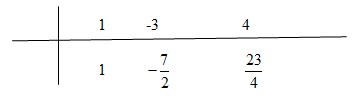
Vì \(\mathop {\lim }\limits_{x \to \pm \infty } \left[ {y - \left( {{x \over 2} - {7 \over 4}} \right)} \right] = \mathop {\lim }\limits_{x \to \pm \infty } {{23} \over {8\left( {x + {1 \over 2}} \right)}} = 0\) nên đường thẳng \(y = {x \over 2} - {7 \over 4}\) là tiệm cận xiên của đồ thị.
e) TXĐ: \(D =\mathbb R\backslash \left\{ { - 1;1} \right\}\)
* Vì \(\mathop {\lim }\limits_{x \to \pm \infty } y = 0\) nên đường thẳng y = 0 là tiệm cận ngang của đồ thị.
* \(\mathop {\lim }\limits_{x \to {1^ + }} y = \mathop {\lim }\limits_{x \to {1^ + }} {{x + 2} \over {\left( {x + 1} \right)\left( {x - 1} \right)}} = + \infty \) và \(\mathop {\lim }\limits_{x \to {1^ - }} y = \mathop {\lim }\limits_{x \to {1^ - }} {{x + 2} \over {\left( {x + 1} \right)\left( {x - 1} \right)}} = - \infty \) nên đường thẳng x = 1 là tiệm cận đứng của đồ thị.
* \(\mathop {\lim }\limits_{x \to {{\left( { - 1} \right)}^ + }} y = \mathop {\lim }\limits_{x \to {{\left( { - 1} \right)}^ + }} {{x + 2} \over {\left( {x + 1} \right)\left( {x - 1} \right)}} = - \infty \) và \(\mathop {\lim }\limits_{x \to {{\left( { - 1} \right)}^ - }} y = \mathop {\lim }\limits_{x \to {{\left( { - 1} \right)}^ - }} {{x + 2} \over {\left( {x + 1} \right)\left( {x - 1} \right)}} = + \infty \) nên đường thẳng \(x = - 1\) là tiệm cận đứng của đồ thị.
f) TXĐ: \(D =\mathbb R\backslash \left\{ { - 1} \right\}\)
* Vì \(\mathop {\lim }\limits_{x \to \pm \infty } y = 0\) nên \(y = 0\) là tiệm cận ngang
* \(\mathop {\lim }\limits_{x \to {{\left( { - 1} \right)}^ + }} y = - \infty \) và \(\mathop {\lim }\limits_{x \to {{\left( { - 1} \right)}^ - }} y = + \infty \) nên \(x = -1\) là tiệm cận đứng.
