Bài 39. Cùng các câu hỏi như trong bài tập 38 đối với đồ thị của hàm số sau:
a) \(y = {{{x^2} + x - 4} \over {x + 2}}\) b) \(y = {{{x^2} - 8x + 19} \over {x - 5}}\)

a) \(y = x - 1 - {2 \over {x + 2}}\)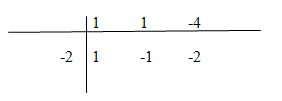
TXĐ: \(D =\mathbb R\backslash \left\{ { - 2} \right\}\)
\(\mathop {\lim }\limits_{x \to {{\left( { - 2} \right)}^ + }} y = - \infty \) và \(\mathop {\lim }\limits_{x \to {{\left( { - 2} \right)}^ - }} y = + \infty \) nên \(x = -2\) là tiệm cận đứng.
\(\mathop {\lim }\limits_{x \to \pm \infty } \left[ {y - \left( {x - 1} \right)} \right] = \mathop {\lim }\limits_{x \to \pm \infty } {{ - 2} \over {x + 2}}=0\) nên \(y = x -1\) là tiệm cận xiên.
b) Tọa độ giao điểm \(I\) của hai tiệm cận là nghiệm hệ
\(\left\{ \matrix{
x = - 2 \hfill \cr
y = x - 1 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{
x = - 2 \hfill \cr
y = - 3 \hfill \cr} \right.\)
Advertisements (Quảng cáo)
Vậy \(I(-2;-3)\). Công thức chuyển hệ tọa độ trong phép tịnh tiến vé tơ \(\overrightarrow {OI} \) là
\(\left\{ \matrix{
x = X - 2 \hfill \cr
y = Y - 3 \hfill \cr} \right.\)
c) Ta nói: \(y = x - 3 + {4 \over {x - 5}}\)
Tiệm cận đứng: \(x = 5\); tiệm cận xiên: \(y = x – 3\).
\(I\left( {5;2} \right);\,\,\left\{ \matrix{
x = X + 5 \hfill \cr
y = Y + 2 \hfill \cr} \right.\)
Phương trình của đường cong đối với hệ tọa độ \(IXY\) là \(Y = X + {4 \over X}\).
